• Information for Parents
• Information for Students
• Information for Educators

The Institute for Mathematics and Computer Science (IMACS) is pleased to announce Elements of Mathematics: Foundations, a new series of online courses designed for bright secondary school students. EMF is a self-contained program that allows the talented student to complete all of middle and high school mathematics up to Calculus before leaving middle school. The curriculum is the result of more than a decade of research and development by an international team of mathematicians and educators and has been in use with gifted and talented students for over 20 years.

Acceleration vs. The EMF Approach

For mathematically talented schoolchildren, subject acceleration is an oft-advised tool for addressing their need to learn more challenging material. Through subject acceleration, a student works on math curriculum that is normally taught at a higher grade level. While acceleration does help bright students avoid repetition of material in which they are already proficient, by definition it cannot help them avoid the tedium that is the standard US mathematics curriculum.

EMF is not an accelerated version of the standard US mathematics curriculum. Instead it provides a deep and intuitive understanding of foundational concepts. This allows the suitably talented child to progress quickly through material for which others would require significant drill and practice. The curriculum then proceeds to cover concepts in a mathematically consistent way, going well beyond the typical gifted math class offered in schools or online. Topics from the standard curriculum – and much, much more – are taught in an intellectually engaging way.

Six Ways In Which EMF Is Unique

• The EMF curriculum was designed from scratch specifically for gifted and talented children to leverage their advanced capacity for learning and to engage their unique ways of thinking.

• EMF provides a deep, intuitive, and lasting understanding of mathematics as a cohesive body of knowledge that opens the door to scientific discovery and technological advancement.

• EMF focuses on the powerful and elegant ideas of mathematics, the kind that gifted and talented children find deeply satisfying and inspiring.

• The EMF curriculum exposes students to subject areas not found in the standard curriculum such as operational systems, set theory, number theory, abstract algebra, and probability and statistics.

• EMF maintains a level of mathematical rigor found typically at the university level while making advanced concepts accessible and fun for a younger audience.

• EMF gives students a true sense of what it takes to excel in college math courses, which is not the same as the skills needed to do well in standard math classes or at math competitions. EMF students do not have to “unlearn” certain habits before they can move forward with more rigorous math courses.

Is EMF Right For Your Child?

EMF courses are self-study and require a certain level of intellectual maturity. Talented students who have completed all of elementary school math but have not yet completed algebra and geometry would gain the most from EMF. However, students who already have some experience of algebra and/or geometry may still find benefit because EMF introduces concepts that are not covered in standard high school mathematics classes.

Parents who register their child at www.elementsofmathematics.com will be offered the option of having their child take a free online aptitude test to help determine their child’s level of readiness.

Whatever your political leanings, it’s clear that the anti-1% movement in the US continues to take its toll on Mitt Romney’s chances of becoming president. Are there similar negative feelings toward the intellectual 1% in our country? Chester Finn, Jr.’s recent op-ed in The New York Times entitled “Young, Gifted and Neglected” echoed a sentiment widely felt in the gifted and talented community for a long time now. Support, both financial and non-financial, for publicly funded gifted schools and programs has always been woefully inadequate. The struggle to keep such programs going is one with which we at IMACS are deeply familiar. (Read about our history in the public sector here.)

As Mr. Finn points out, one of the most common but inaccurate criticisms of gifted programs is that they are “elitist.” In math and science, related obstacles to greater support are (1) a lack of understanding of how important these fields are to sustaining and improving the quality of life for us and generations to come and (2) unrealistic expectations about how and when the payoff from supporting talented children comes. Some of this is rooted in the sad state of math and science literacy in the US, and some is influenced by our always-on media culture.

At IMACS, we’re the first to celebrate advances in technology, but one undeniable consequence of our “insta-world” is that people want to see the results of their actions right away. The same may be true of the tax-paying public. By definition, the large majority of parents do not have gifted children. Human nature is such that people are inclined to advocate for what benefits themselves or their own. So how do you convince them that it’s worth supporting someone else’s kid because five or ten or 20 years from now, he or she may discover the cure for a disease that someone they care about might suffer from one day? This is a mighty challenge, but that’s what the gifted and talented community specializes in, whether it’s the amazing work our kids do or the tireless advocacy of their parents on their behalf.

As one “science guy” recently put it, “We need scientifically literate voters and taxpayers for the future.” While raising math and science literacy over time is the best long-term solution for everyone, gifted or not, that doesn’t help today’s bright kids whose growth years are ticking away. It certainly would help if media outlets gave as much exposure to Taylor Wilson’s nuclear research as they do to Taylor Swift’s love life. Let’s get out there as parents and educators unabashedly shining a positive light on our best and brightest students. After all, they’re not here to ruin the curve but to improve people’s lives by solving the toughest problems. There shouldn’t be any doubt that this 1% will give back to society many times over.

Editor’s note: Going forward, The IMACS Blog will be published every four weeks with our next post appearing on October 25, 2012. Thanks to all our readers for your continued support!

It’s the middle of September, so your school-aged kids are likely back in the rhythm of classes, extracurricular activities, homework, and maybe even part-time jobs. Busy schedules are taking shape, and the effort to fit everything in will likely mean some trade-offs. To the extent that your kids still look to you for help with their homework, take this moment to remember (or learn) this: Letting your children struggle at first will lead to better outcomes than if you simply provide the answer in the name of expediency.

In a study published earlier this year, education researchers compared the performance of math students in two groups. One group was given direct instruction when learning a new concept. In other words, they were told at the start how to solve a new type of problem. The second group was given the problem and asked to come up with as many approaches to solving it as they could before receiving any formal instruction. In several comparisons, researchers found that both approaches were effective at imparting basic knowledge of the new concept. However, students in the second group formed a much deeper conceptual understanding and were better able to transfer their knowledge to different situations.

This was the case even though the second group usually failed to come up with a completely correct solution. Researchers call this approach “productive failure.” Their study also showed that a higher number of incorrect solutions correlated to increased learning when those students were finally given instruction on the topic. The more we struggle to figure something out, the better we understand it when we finally do understand it. Why is that?

The theory behind the difference in performance has to do with the learning process. It seems that when we try to solve a new type of problem without new information, our brains have to lean on what we already know. When we are finally presented with correct approach, our brains make connections between the existing knowledge that was called up and the new knowledge. This seems to be a fundamental part of successful long-term learning.

Here’s the sad part for American students and where you, as parents, can try to help your kids. Math education in the US typically follows the direct instruction model. By contrast, consider how students in countries that outperform the US in math learn a new mathematical concept. The section of the video below that starts at about the 1:43 mark discusses the TIMSS 1999 Video Study of eighth-grade mathematics and science teaching in seven countries. Consistent with the “productive failure” study, the TIMSSS videos showed that teachers in countries that outperform the US allow their students to struggle with new math concepts first.

In the best case, your child’s teacher already uses the “productive failure” approach. Keep up the good work at home when it comes to homework help. If the teacher uses direct instruction, then try encouraging your child to think of various ways of approaching the problem before attempting to explain the teacher’s way. Many of us at IMACS are parents too, so we know this is easier said than done with the busy lives that kids and parents lead today. In the long run though, it’s well worth the effort.

In our previous IMACS blog post, we began our response to Professor Andrew Hacker’s op-ed piece entitled “Is Algebra Necessary?” by taking a critical look at his reasoning in favor of eliminating the requirement for high school algebra. We argued instead that the approach to teaching algebra, and more broadly all of mathematics, should be changed significantly in the US to benefit all students, from those who are struggling to ones who are at maximum achievement under the current limited system. In this week’s post, IMACS discusses key elements that we believe should be part of any effective curriculum in mathematics.

We were pleased to see that Prof. Hacker quoted mathematics professor Peter Braunfeld of the University of Illinois as saying, “Our civilization would collapse without mathematics.” Prof. Braunfeld is not new to the mathematics education debate, having co-authored an article* on the subject with IMACS principal founder, Burt Kaufman, and IMACS curriculum contributor, Professor Vincent Haag, nearly 40 years ago. (Prof. Braunfeld was also a contributor to the IMACS curriculum.) Their article outlined five principles that have and continue to guide IMACS in our curriculum development.

Everything Old is New Again

A 40-year-old article!? How can that be relevant now? Sadly, the circumstances lamented then by the co-authors remain a plague on our US math curriculum to this day. Have you heard anything like the following excerpts lately?

It’s no wonder that students find math dull and tedious. The trivialized curriculum forced upon them has been stripped of all the wonder and beauty of mathematics.

In just the past year, the articles we’ve read suggesting that video tutorials, massive open online courses, and the iPad are going to “revolutionize” education are too many to count. The drive-thru window may have changed how Mickey D’s was served, but the stuff in the paper bag remained of questionable nutritional value for a long time. (Yet even the Golden Arches eventually overhauled its menu!)

Can we say teach to the test? The idea of “industrialized education” came about long before No Child Left Behind. What’s unfortunate is that such an ill-conceived notion wasn’t what was left behind.

Five Guiding Principles of Mathematics Education

So what are the five guiding principles that the co-authors proposed? The excerpts that follow summarize how they believed mathematics should and can be taught to children and how IMACS teaches today:

Exasperated students continue to ask when they are ever going to need high school math in the real world, and who could blame them? Yet you never hear such broad and fervent protest about high school science even though relatively few kids will put that knowledge to work. Why less complaining? Because science curricula, for the most part, still incorporate grand ideas that elicit awe in young minds. Why are parents appalled by cuts in the arts at school? Not because most think their kids will pursue careers in creative fields, but because they understand that the aesthetic experience lifts the human spirit.

Mathematics is brimming with this kind of elemental beauty too. Yet decade after decade, schools use curricula that deprive math students of the good stuff. It’s like feeding the cardboard box instead of the cereal to a kid and saying “See, it says ‘cereal’ right there on the label. How can you say it’s tasteless?” Children have been telling us for too long that we need to change the menu. It’s time we listen.

*”Mathematics Education: A Humanist Viewpoint,” Braunfeld, Peter, Burt A. Kaufman, and Vincent Haag, Education Technology, November 1973.

Editor’s Note: IMACS will soon be rolling out a series of interactive online math courses designed with the five guiding principles discussed above. These courses will allow talented students to complete all of middle and high school mathematics with the exception of calculus before leaving middle school. Check back at www.eimacs.com or like us on Facebook for exciting details to come!

Andrew Hacker, emeritus professor of political science at Queens College, City University of New York, recently wrote an op-ed piece in The New York Times entitled “Is Algebra Necessary?” His opinions caused quite a stir in the ongoing debate over mathematics education in the US. IMACS sees value in some of his ideas, such as teaching quantitative reasoning starting in kindergarten, and we agree that schools should not subject students to the “ordeal” of struggling with algebra. However, IMACS believes that education professionals should focus on changing the way mathematics is taught, not on eliminating the requirement to study algebra.

First, consider the attendant consequences of the author’s proposal, which is to create alternative math courses that “familiarize students with the kinds of numbers that describe and delineate our personal and public lives.” Perhaps the large yet still minority percentage of students who cannot pass traditional algebra would be allowed to satisfy their high school math requirement with these alternative classes. As the author sees it, this would limit “misdirecting precious resources” presumably by redirecting them to the new classes. Does that mean we abandon the majority of students who can pass traditional algebra to the ineffective mores of a failing system (now with even fewer resources) because, hey, at least they’re not struggling? Never mind the fact that neither are they soaring as high as they could and will need to as the influence of technology on their world grows!

Teaching mathematics effectively to all students is the outcome we should be striving toward. Make no mistake—we understand the consequences of the prolonged economic stress on families, school districts, and public higher education. It is natural in such times to direct limited resources to activities most likely to lead to gainful employment. So let’s consider a key element of the author’s argument—that high schools are not even teaching students the math skills they will need in the workplace. He writes:

The author seems to miss the point that the mathematical reasoning skills needed to succeed in the workplace are the same ones needed to succeed in algebra. In both cases, you must be able recognize a problem or challenge, gather information relevant to finding a solution, analyze and synthesize the information to derive a solution, and effectively apply the solution. This takes critical thinking and logical reasoning abilities, and the current pedagogical approach is to try to impart these skills through the process of teaching algebra, almost as a side-effect.

Were the US education system to focus more in elementary school on building these fundamental skills, not only would students find learning high school algebra (and learning in general) easier, they would also be better equipped to succeed in the workplace where problem solvers are highly valued. Furthermore, as learning algebra becomes easier, it becomes less time-consuming, thereby freeing up instructional time to add topics from skill-training to more advanced math as desired. It may sound like an idealistic vision to the millions of people who have come to believe they are “bad at math” when they are more likely the product of bad math curricula, but we have seen this approach work for IMACS students for over 20 years.

Of course considerable training occurs after hiring in STEM fields! The need for accuracy and the complexity of the body of knowledge are so much greater in these fields than in others that are more subjective in nature (e.g., the arts) or that rely more on so-called “soft skills” (e.g., politics). We need only to look to the history of the Space Shuttle to understand the consequences of errors in judgment. On a happier note, consider that the successful entry, descent, and landing of the Mars Science Laboratory was almost 10 years in the making. On-the-job training is necessary in many non-STEM fields from law to portfolio management to journalism to costume design. Why should we expect STEM be any different?

As for the Toyota-sponsored Machine Tool Mathematics class, the course catalog description is “An applied mathematics course designed for machinists which includes instruction and practice in algebraic and trigonometric operations. (2 hour lecture, 2 hour lab).” That doesn’t sound like the math is different from what is taught in high school. Rather it sounds more like the way the math is taught is different. With a hands-on lab, it actually sounds like fun! That is a huge distinction and goes back to our main point that we need to significantly change our approach to how we teach mathematics in the US.

At IMACS, we support the idea of schools using math curricula that accurately incorporate real-world examples that students care about. This approach helps put abstract concepts in context but, more importantly, gets students interested in learning and helps them understand how mathematics shapes our world. Those who appreciate mathematics in its pure and abstract form are pretty special people, but math should and can be accessible to the majority as well. There also need to be more options for visual-spatial learners who may not “get” math concepts when presented on a bland white board. Rather than redirecting limited resources to creating new alternative classes, the focus should be on redesigning the algebra curriculum (as well as those for elementary, middle, and the rest of high school math) to present mathematics for what it truly is, a deep discipline centered around simple but beautiful ideas, rather than a bunch of numbers, funny symbols, and boring algorithms.

The IMACS Blog has recommended several games, puzzles, and apps that encourage structured mathematical or computational thinking. We’ve also noted the benefits of unstructured time for creativity and for inspiring insightful problem solving as supported by a 2009 study on wandering minds. This week’s blog brings together these two ideas with a look at a puzzle called the Ball of Whacks. This toy was recommended to us by an IMACS alumna whose daughter is enrolled in our Primary Enrichment math class, so we have it on good authority that the Ball of Whacks is a winner!

What Is It?
The Ball of Whacks is a puzzle that consists of 30 magnetic pyramids, which the inventor calls “Whacks.” When you open the package, the 30 pieces are held together by internal magnets in the form of a ball-like, 30-sided rhombic triacontahedron. Give the “ball” a good whack and it will break apart so that you can play with the pyramid pieces.

What makes these pyramid pieces so special? Each is a right golden rhombic pyramid! (We math geeks tend to have a natural appreciation for toys such as this one.) As the mini-book that comes with the Ball of Whacks explains:

Space Out
Whether you’re an aficionado of this special polyhedron or what you’ve read above is enough to satisfy your mathematical curiosity, we think you will enjoy playing with this toy in several ways. After breaking the puzzle apart, your natural first instinct may be to figure out how to put it back together. Although this won’t be challenging for most of our blog readers, we think you’ll still find it satisfying if you enjoy the simple beauty that mathematics often presents.

With that out of the way, you might find yourself casually shifting puzzle pieces around without much physical effort or purposeful direction. Then in what seems like a sudden moment, they come together in one of many interesting shapes or patterns. The experience is reminiscent of doodling as a way of relaxing and unleashing your subconscious. This kind of unstructured play feels uncannily like a physical representation of a wandering mind that experiences sudden insight in solving a problem.

Creative Design
When you’re in the mood to solve a well-defined problem analytically, pick one of the more than 20 shapes in the mini-book and try to make it yourself. Then think outside the book and create your own design. If you enjoy tangrams, then you’ll probably enjoy playing with the Ball of Whacks in this way. Don’t forget that the pyramid pieces are magnetic, so you can create designs on any metallic surface such as a refrigerator door or magnetic white board.

In addition to the shape challenges, the mini-book also contains 15 exercises that make up what is called a “creativity workshop.” For example, Exercise 4 asks you to drop your assumptions about how you play with the Ball of Whacks. As the book explains:

The exercises make for an interesting casual read. They may even help parents begin discussions with children that end up leading to creative thinking. Given that different minds get stimulated by different types of experiences, it’s hard to say definitively that this particular toy will enhance your creativity. However effective the Ball of Whacks is as a creativity tool for a given individual, one thing is certain: the Ball of Whacks is a fun toy for unstructured play, which is widely understood to be good for creativity.

Geometric Gem
The Ball of Whacks can be had for about $25 online through retailers like Amazon. Some might balk at what seems like a high price for a “simple” toy; however this seems to be in line with the price for magnetic “thinking” toys such as Magna-Tiles and Geomags. For a mathematically inclined mind, the Ball of Whacks can be loads of fun!

This scorcher of a summer is only half over. Are your kids bugging you for stuff to do? If you own an iPad, consider these nicely priced apps to keep their minds engaged and entertained. They won’t even realize they’re learning something! We realize this list is hardly complete, so IMACS welcomes your suggestions for similar apps on any platform. The main criteria, which is how we picked these three, is that the app should introduce some type of mathematical or computational thinking in a very natural and intuitive way. No overt instruction. No drilling. Just clever and fun learning!

Cargo-Bot (Free)

Cargo-Bot won’t teach you how to program, but it goes a long way to introducing some of the basic principles of computational thinking in the guise of a fun and addictive game. Each puzzle starts with various colored boxes on a platform and a picture of how the boxes should be situated once the puzzle is solved. Your job is to make the robotic arm move the boxes from their starting position to the prescribed ending position using a set of simple of drag-and-drop commands. The trick is to complete the task using the fewest number of instructions. That’s right, you get more points for shorter programs!

In addition to surreptitiously introducing the basics of stacking, sorting, looping, if-then statements, and calling another program, Cargo-Bot forces you to think carefully about your “code.” You might succeed in moving the boxes to their correct destination, but with anything less than the ideal solution you’ll come up maddeningly short of the maximum stars awarded. Your program might also cause the claw to do something unpleasant like smash into a wall. You simply can’t help but want to remedy these situations. In other words, the app makes you want to debug your code or make it more efficient. Brilliant!

Symmetry Shuffle ($1.99)

Symmetry Shuffle is a visually beautifully app that tests your spatial reasoning abilities. Use your fingertips to slide (translation), flip (reflection), and turn (rotation) an asymmetric master image across a board made up of similar background images positioned with different orientations. See with your mind’s eye and your actual eyes what happens to the master image under these geometric transformations. Each time you move the master image over a background image so that they match in orientation, the monotone background image becomes artfully colorful. Complete all matches to solve a puzzle.

The puzzles can be played in two modes. In Race Mode, you try to score as many points as you can before the clock runs out. One point is awarded each time you make a match. Unused time from the previous level is added to the total time allotted to solve the next level. In Solve Mode, you try to solve the puzzle using the fewest moves. Even the toddler/preschool set could appreciate this game. There is really no need for verbal explanation. The touch commands are so intuitive that a few examples make clear what to do.

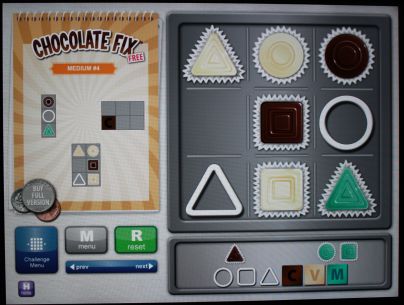
Chocolate Fix Free (Free) and Chocolate Fix ($2.99)

We’re eternal fans of the ThinkFun’s Chocolate Fix game, both the physical version and the app. (Could it be because IMACS alumus Mark Engelberg is the developer?) This perennial favorite of our students makes learning logic so much fun! The rules of the app are the same as the physical game. Color and shape clues offer incomplete information about the location of each confection in a 3×3 tray. Use your logical reasoning skills to determine where each of the nine pieces go.

Chocolate Fix Free contains 30 challenges across four levels of difficulty (15 easy, 10 medium, 3 hard, and 2 expert), whereas Chocolate Fix contains 100 challenges at each level for a total of 400. For the very young or the logic novice, one great aspect of the app is that you can click on the “Hint” icon to get just a bit of help. With the physical game, it’s difficult to get hints because flipping over the challenge card reveals the entire solution on the back.

Enjoy the rest of your summer!

Are you interested in learning to play chess? Is your child? Teen chess champion and IMACS student, Rachel Gologorsky, shares her advice on how to get started. Read more about Rachel’s journey from curious toddler to 2011 US Girls Junior (U21) Chess Champion in her previous blog post.

It’s really easy to be good at chess if you start the right way and with the right foundation. That’s how my father taught me after my mom explained the object of the game and how to move the pieces. He taught me to first focus on the last, i.e., the endgame. If you know where you want to go, the rest becomes easier—it is just a matter of execution.

Endgames

The endgame is the end stage of chess games, commonly defined as when there are fewer than six pieces on the board. There is so much to learn in endgames, but Jeremy Silman’s book, Silman’s Complete Endgame Course, is an excellent tool for learning all the endgame ideas one needs to know from beginner to master.

Focusing first on the endgame is helpful because it highlights how the pieces coordinate together. When there are so few pieces it’s easy, especially for a beginner, to see how each of her moves affects the opponent’s move and how that, in turn, affects her next move.

The first thing that beginners should learn in endgames is how to win, that is, how to put the opponent in checkmate. A checkmate, or “mate” for short, occurs when a king is under direct attack and cannot avoid being captured.

Studying how to put the opponent’s king in mate helps a player to learn the relative power of different pieces and to sharpen her ability to create mating nets. Creating mating nets is the process of methodically restricting the options of the opponent’s king until, at last, the king is put in mate.  These nets are especially pleasing to players with an innate sense of geometry, structure, and neatness. This is because mating nets are usually created by methodically repeating the same geometric structure in a precise move order, leaving nothing to chance in the quest to mate the opponent’s king.

These methodical moves are actually plans, and the concept of plans and planning becomes an engraved tenet in the foundation of the young player’s mind. Later on the ideas of plans and planning become an important component of playing chess strategically.

After I mastered the basic endgame checkmates (how to mate the opponent’s lone king with any of the following combinations: (1) king and queen, (2) king and two rooks, (3) king and rook, (4) king and two bishops, and (5) king, bishop, and knight), my father added another component to our program: tactics.

Tactics

A tactic is a sequence of moves which limits the opponent’s options and may result in tangible material gain. Tactics occur in patterns—the move sequence may be different, but the overall idea is the same. There are many different kinds of tactic patterns, but all are built on the most basic “skeleton” patterns. Those are:

The fork: A fork occurs when a single piece attacks two pieces at once.

The skewer: A skewer occurs when one of your pieces attacks two of the opponent’s pieces in a line, where the more valuable piece is in front of the second piece. The opponent is forced to move the more valuable piece to avoid its capture, thereby exposing the piece behind it, which can then be captured.

The discovered attack: This attack is revealed when one piece moves out of the way of another piece. The discovered attack can be very powerful, as the piece moved can make a threat independently of the piece it reveals. They succeed because the opponent is unable to meet the two threats at once.

Indeed, every one of the above tactics relies on a double threat or a double attack, as it is most commonly called. That is the basic idea of every tactic played, whether the tactic is played by beginners or grandmasters (GM). Indeed, GM Yuri Averbakh, the oldest living GM in the world, stressed in his Chess Tactics for Advanced Players that “the double attack is in one form or the other is [sic] the basis of [even the] most intricate tactical operations.”

Learning and finding these elemental tactical patterns in positions is vital to a player’s development because doing so etches those patterns in the player’s mind. Once you own these patterns, you can recognize them in games. This allows you to turn lost games into winning ones and avoid turning winning games into lost ones.

You can also build on these patterns and combine them to create potent combinations that, over a sequence of moves, force your opponent at the conclusion to lose something. The sequence of moves could force a checkmate, or force the opponent to lose material (valuable pieces or pawns), or force the opponent to give up a strategic asset. Making use of tactics to build up a combination in which I give up all of my pieces but one—the one that forces mate—is beautiful. Those combinations hold an aesthetic value for me, and that makes them fun to see and even more fun to play.

My father always opened our tactics book last so that the end of our chess sessions was always the most fun. Today, however, free websites like Chess Tempo are becoming preferable to tactics books. Not only is there virtually no limit to how many tactical puzzles one can access, the tactical puzzles are chosen on a bell curve with consideration given to your rating. This way, the difficulty of the puzzles grows with your strength.

After I grasped the basic tactical patterns, my father added a completely new dimension to our sessions: strategy. This too, in a way, is working backwards because implementing strategy allows one to coordinate one’s pieces favorably. And when that happens, tactical strikes usually appear that make use of the positions of the pieces.

Strategy

Strategy is the aspect of chess playing that is concerned with the evaluation of chess positions and the setting of goals and long-term plans for future play. Strategy is basically about playing better chess than your opponent and, in chess slang, is called “outplaying the opponent.” Jeremy Silman’s book, How to Reassess Your Chess, is a wonderful guide for learning a logical approach to strategy.

Strategy becomes more important as a player’s skills progress because the players are less likely to miss or be felled by a major tactical blow. Thus, decisive games rely more on which player can outplay his opponent. Outplaying an opponent can only be done with a good grasp of strategic concepts (I still haven’t figured out all of them), some of them being:

Strategy, if implemented correctly, can also be beautiful. Unlike flashy tactics, however, strategy is deep and cannot be spotted easily. Finding strategic ideas and implementing them gives a player a sense of confidence, appreciation of the game, and satisfaction because a win based on strategy means that your opponent didn’t make any mistakes at all—you just outplayed them!

Openings

Finally, my father turned his eye toward openings. An opening is how you start the game and usually lasts for around 10 moves or so. Openings are important in the sense that you want to start a chess game off on the right foot. One has to know openings in order not to lose the game right of the bat.

Nowadays, some of the more advanced players don’t spend much time on openings because they already know the general principles. The most advanced players (grandmasters), however, have to know openings deeply because the slightest inaccuracy will be capitalized on by their opponents. If you’re just starting out in tournament chess, you will most likely play beginners. But even they are becoming more and more “booked up” (i.e., know many opening variations). Although I don’t recommend studying openings too much as a beginner, I do recommend studying the main opening you play enough to know its major guiding idea. That way you can parry any prepared move logically and stay out of trouble.

There are those who will try to catch you in traps. Although better, logical play should and will eventually prevail, it’s useful to know common “trash trap” lines (i.e., a sequence of opening moves that sets a trap for you to fall into, but usually damages the position of the opponent who sets it). You will lose if you don’t see the “trash trap,” but if you know the trap, you will be able to counter it in such a way as to capitalize on your opponent’s damaged position.

It’s good to learn and play mainstream open game openings. Open game openings are characterized by one or more of the following:

(a) Open files (the squares running down a board)

(b) Open diagonals (the diagonals running across the board)

(c) Fluid (easily exchangeable) or absent center pawns (pawns on the e4/d4/e5/d5 squares; Click here for a complete explanation of the algebraic notation used in chess.)

(d) Tactical devices playing a major role

(e) Possibilities of gambits (openings in which one side gives up material for some sort of compensation)

(f) The first move played is the king’s pawn moving two squares forward. (In algebraic notation, the move would be expressed as 1.e4.)

These openings are educationally important because they show clearly many strategic elements, such as methods of:

Openings also highlight elements that have both strategic and tactical components, such as the importance of tempi (the interplay of time and moves), plans, and counterplans. These things are usually explained very well in most opening books. Chess Openings for White, Explained and its companion volume, Chess Openings For Black, Explained do an exceptionally good job of explaining opening ideas.

Practice and Learn

If one is serious about chess one should also play in rated USCF (United States Chess Federation) tournaments, if only to test the ideas out in action and to track progress. Since it’s often impractical to go to tournaments more often than once a month (unless there is a chess club nearby), I recommend either playing games in the meantime on the free ChessCube website, or buying a membership to the Internet Chess Club (ICC, $30 per year). In my experience, ICC has better interfaces, graphics, and is generally easier to navigate and understand than other chess servers. But the main point is that one has to play games often in order to track progress and improve.

As the player’s skills improve and s/he reaches a class D (1200-1400) tournament rating, hiring a private coach can be of an enormous help. My current coach, GM Alexander Shabalov, a four-time US chess champion, has been instrumental in analyzing my games, explaining new opening ideas to me, and pinpointing my weaknesses and misconceptions.

Finally, although Zermelo’s theorem in game theory proves that chess can be “solved” in the sense that the game’s final outcome can be forced, chess is still a game of so many possibilities that understanding its intricacies is a lifelong endeavor. I know that throughout my lifetime, my attempt to understand chess better will be a journey of constant learning. And, that is my goal: to learn all I can, in chess and in the world in general.

Editor’s Note: The IMACS Blog will return on Thursday, July 19th. If you’re celebrating during 4th of July weekend, have a happy and safe time!

Can it really be that almost a year has passed since our very first ‘Staff Picks’ blog post? That means another class of IMACS graduates is moving on to new adventures in learning, and we are busily planning for our Hi-Tech Summer Camp. It also means that it’s time to meet three more members of our IMACS family—Daniel Payne, Ken Matheis, and Lauren Rosenfarb—and to get their book and movie recommendations for this summer.

Daniel Payne, Assistant Director and Senior IMACS Instructor

Dan has been teaching for IMACS since 2003. He teaches all levels of math and computer enrichment and our University Computer Science I course. In addition he teaches many of our Placement Classes for new students. Dan is very enthusiastic in everything he does and it shows as his students love his classes and always hope that he’ll be teaching them again the following year. Dan received his BA degree in Anthropology from Florida Atlantic University and also has an extensive IT background.

Here are Dan’s picks:

“My favorite book is The Hacker Crackdown by Bruce Sterling. It’s a true crime story about the the dawn of computer hacking as a romanticized pursuit for teenagers. These were my contemporaries, and as a part-time denizen of the electronic BBS culture, I felt connected to the stories in this book. Sterling dissects the lives of the ‘villains’ to walk the reader through what lead the kids to commit these crimes and how the FBI was in way over their heads trying to catch them. There is something special about the electronic ‘nerd’ culture heroes who were only known by a select few until the movie The Matrix formalized this appeal to the masses in 1999.

That leads me to my favorite math/science movie. Yes, The Matrix. Pop culture latched on to the visuals, but for me that is only a bonus. It was the right movie at the right time, bridging the shift in the meaning of ‘nerds’ from a pejorative for socially awkward brainiacs to exceptional, savvy people who know how to do important things the rest of us do not. The protagonist, Neo, a hacker superhero, could not have existed on screen ten or even five years prior. The few movies that tried it were unable to capture the hacker/gamer culture that had already existed on a small scale for decades. Yet he seems perfectly believable ever since.

One more thing. The film was an excellent vision of Rene Descartes’ ageless dilemma that there can be no proof that our world is as our senses inform us. This is another well trodden topic that the Wachowski siblings did better in this film than any other rendition I have seen or read.”

Ken Matheis, Senior IMACS Instructor

Ken is a senior instructor for our computer science program. Ken was a student in Project MEGSSS, the predecessor program to IMACS, through 11th grade. When MEGSSS lost its public funding for his senior year, he completed his courses at IMACS as one of our first group of students! Ken received bachelor’s degrees in Mathematics and in Electrical and Computer Engineering from Rice University. He was a part-time IMACS instructor from 2000 through August 2011. During part of this time, Ken completed his MS and PhD in Mathematics with a specialization in Cryptography. Since September 2011 Ken has been working full-time with us as an instructor and also as a programmer working on several important projects, including our ISLANDscience virtual science lab.

Here are Ken’s picks:

“For my favorite TV series, I have to go with Star Trek. No matter which spinoff series you watch, you see Gene Roddenberry’s vision of what humanity could accomplish if we got over our minor differences and worked collectively to solve the more serious problems we face, such as widespread hunger, severe poverty, and abject racism. Equally important, the characters also demonstrate the right attitudes one should have when resolving conflicts: cooperation over stubbornness, empathy and diplomacy over aggression, understanding over ignorance. Sure, there are plenty of physical conflicts as well, but entering into them is depicted as a last resort.

My favorite book is The Foundation Trilogy by Isaac Asimov. The Foundation Trilogy focuses on the application of mathematics to human psychology with the goal of predicting human reactions to various events. Such a project is breathtaking in scope, requiring statistical analyses of quadrillions of humans. The outcomes, however, only apply to groups of people; they do not and never can predict the reactions of a single individual. Asimov tells a masterful tale of a 30,000 year old collapsing galactic empire and a protagonist who uses this technique to attempt to rebuild it in a mere thousand years. It inspires me to push the limits of mathematics in my own fields in order to benefit our society.”

Lauren Rosenfarb, Marketing Director

Lauren began her IMACS career in 2005 as an instructor. She is now our Marketing Director and also manages our homeschool programs. Lauren graduated from the University of North Carolina at Chapel Hill with a degree in Public Relations and Journalism and Mass Communication. We love having such multi-talented people on our staff!

Here are Lauren’s picks:

“I really enjoyed many of the math and science focused books and movies previously mentioned in our ‘Staff Picks’ segment. Two additional math and science movies definitely worth watching are Moneyball and Contact.

Moneyball, originally a book by Michael Lewis, is based on the true story of Oakland Athletics baseball general manager Bill Beane (portrayed in the movie by Brad Pitt). After loosing many of his star players, Beane has to reassemble a ball club despite an almost impossibly tight budget. Beane hires Jonah Hill’s character, Peter Brand, a young, Ivy League economics grad, with radical ideas about building a winning team. Using statistical analysis, Brand and Beane find a whole team of undervalued players and invest, not in stars, but rather in probable hits and runs – the stuff that wins are made of. The idea of valuing statistical data and probabilities over intuition and experience does not sit well with Beane’s scouts and controversy ensues.

Mathematics also plays an important part in the movie Contact, based on the Carl Sagan novel of the same name. In the movie, Jodie Foster’s character Ellie uses radio antennas at the Search for Extraterrestrial Intelligence project (SETI) to listen for any radio signals coming from space in hope she will discover a message from intelligent extraterrestrial life forms. After years of detecting nothing but natural random radiation, Ellie finally picks up a transmission that consists of the first 261 consecutive prime numbers. Because there is almost no chance of that sequence of prime number randomly occurring in nature, Ellie theorizes that the radio transmission must have been created by an extraterrestrial intelligent life form.”

Dan, Ken, and Lauren – thank you for sharing these books and movies. Our blog readers will surely enjoy these thoughtful suggestions.

Note: This story is adapted from the IMACS “Elements of Mathematics” series of textbooks and is based on modular arithmetic. This topic is typically covered in the first year of EM, which is often taught to talented 6th graders. The solution is revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!

The Stolen Jewel of Rainsmore
In the town of Rainsmore someone has stolen a precious jewel. A very famous detective, Roy Henshaw, has been called in to solve the crime. After a great deal of questioning, Detective Henshaw has narrowed the number of suspects to a small group.

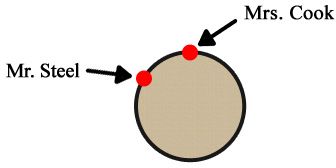
Late Wednesday night Henshaw seats the suspects around a table and begins questioning with Mr. Steel. Then he questions Mrs. Cook.

After Mrs. Cook has been questioned, Henshaw continues around the table in order, being very careful to skip no one and to ask each person a different question.

The questioning continues through the night with Henshaw getting closer to finding the thief.

By 5:00 in the morning Henshaw has asked hundreds of questions and, being such a famous detective, he has kept track of which questions each suspect has answered:

Mr. Steel has answered questions 1, 8, and 15.
Mr. Gunn has answered questions 3, 10, and 17.
Mr. Decker has answered questions 12, 19, and 26.
Mr. Jones has answered questions 11, 18, and 25.
Mrs. Cook has answered questions 2, 9, and 16.

Henshaw now has some important questions for which he needs answers. You should answer them if you are to solve the mystery.

a) How many people were seated around the table?

b) Who answered the 4th question?

c) Who answered the 5th question?

d) Who answered the 24th question?

e) Who answered the 31st question?

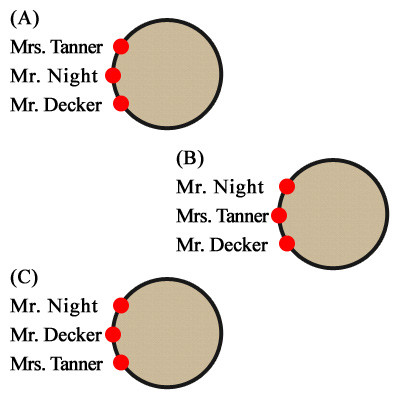
f) Detective Henshaw also noted that Mrs. Tanner answered question 70 and that Mr. Night answered question 48. Which of the following pictures shows the correct seating around the table of Mr. Night, Mrs. Tanner, and Mr. Decker?

g) Aha! Henshaw now knows who the thief is. His extremely clever and searching mind has unmasked the criminal.

THE CRIMINAL IS NONE OTHER THAN THE PERSON WHO ANSWERED THE 37TH QUESTION.

Who is the thief?

Has traditional school stolen your passion for learning? Find it again with engaging courses in gifted math and computer science online from IMACS! Register for our free aptitude test. Play along with our weekly IMACS logic puzzles on Facebook.

Answers:
a) Seven
b) Mr. Jones
c) Mr. Decker
d) Mr. Gunn
e) Mr. Gunn
f) Table (A)
g) Mrs. Cook