• Information for Parents
• Information for Students
• Information for Educators

Originally published in the May 1992 issue of The Computing Teacher, this essay by IMACS alumna Natasha Chen brought much needed attention within computer science education circles to the debate over teaching computer programming for beginners. Amazingly, almost 20 years later, the key issue raised by the article – how to teach fundamental computing concepts in a way that is effective, engaging and empowering – remain unresolved. Many students still find themselves in syntax-driven classes that focus on a short-term ability to “make apps now!” in the language du jour rather than being taught strong fundamentals that enable success throughout college and career, regardless of which programming language is used. At a time when the US faces a huge gap between technical job positions and qualified individuals to fill them and the UK is grappling with a need for true computer science in its national curriculum, IMACS revisits this issue with a renewed urgency.

A Bad Beginning In BASIC
My first experience in computer programming classes was an elective course in BASIC back in sixth grade. I chose that class because I thought that computers were powerful and capable of doing many interesting things. Electives usually have a reputation for being fun, but my classmates and I heard stories about the difficulty of this course and how only one or two kids ever got A’s. I thought to myself, “Maybe they just weren’t interested in computers. But I am, so how bad could it really be?”

Pretty bad! Forget learning anything that encouraged us to think, wonder and explore. We were asked to study the history of computers, memorize the names of hardware, and master the rules of syntax. We were sixth graders. We weren’t about to enter the high-tech world of programming. All we wanted was to see what neat things we could do with the computer. The class wasn’t difficult at all; memorization is hardly a challenge if you take the time to do it. There were so few A’s because no one cared to do busy work, and that’s all that was offered.

Swamped By Syntax
After my sixth grade BASIC experience, I never wanted to take another computer science course again. Of course, when you are eleven years old, G.P.A. and class rank don’t mean much to you. But by the time I was about to enter my junior year in high school, I started thinking about those things … and college … and the classes I needed to take. To avoid another BASIC nightmare, I decided to bypass Computer Programming I (BASIC) and go straight into Computer Programming II (Pascal). Pascal was different enough from BASIC to make me think that it had to be better. I found out that the improvement was far less than I had hoped. We jumped right into the syntax of Pascal: program (input, output), begin-end, etc. Even after two years of studying Pascal, I still can’t remember all the rules.

It’s like trying to interest small children in reading. You try to show how much there is to discover in books by reading with or to them. Maybe they will pick up some books on their own and then some more, and pretty soon they will have built up a library. But if you dump the library on top of them, ask them to memorize the Dewey Decimal System and then put the books back in order, by the time they finish – assuming they do – they won’t care to look at another book, much less read one.

One of the students from that CP2 class had a very hard time with the syntax of writing information-processing programs, but when it came to the one graphics program we were assigned he was an absolute genius. I can’t begin to describe all the amazing things he could make the cursor do. But he was never recommended for the AP Computer Science class. By having no place for such a student, the computer education system may very well be tossing aside some of the best computing minds, simply because they don’t fit the mold of the curriculum whose rigidity derives from that of the languages used.

AP Computer Science: As Good As It Gets?
Five of us made it to the AP CS class and four more came from the CP3 (Fortran) class. We spent the first two days refreshing our memories of the syntactic rules that had evaporated over the summer. It seemed as if the purpose of CP2 was to teach us the rules and now, we had to remember them so that we could play the game – someone else’s game.

The last year was one of frustration. The most commonly heard outburst in our classroom was undoubtedly, “Stupid computer!” No matter what, it was always the computer’s fault. It seemed that my classmates’ programming strategy was to let the computer find their errors in the hope that this would somehow help them solve the problem. It never occurred to them that the computer is simply a testing ground for a well-thought-out idea. A human could conceivably go through an algorithm manually; it would just take an intolerably long time. For most of my classmates, this was their fourth year in the computer science education system, and all it had taught them was to rely too much on the computer and not enough on themselves.

The root of this problem lies in what is currently thought to be important for students to learn in computer programming courses, namely, syntax. Whoever is designing the high school computer science curriculum seems to think that, once students learn the rules of the language they are studying, having them write programs that demonstrate how those rules are applied will teach them what is important in computer science. As a student who has been through the system, who has had to waste the majority of my patience, concentration, and effort on keeping the syntax of my programs straight, leaving barely enough of these qualities to devote to solving the problem, I can tell you that such a belief could not be more wrong. This method of teaching is brainwashing. It is not like brainwashing or similar to brainwashing; it is brainwashing. It is a danger to computer science, sending out trained hackers instead of enthusiastic visionaries. Fortunately for me, I was given the opportunity to recover.

Saved By Scheme
In ninth grade, my math class began an introductory computer programming course in Logo. My classmates and I looked forward to every other Friday when we studied Logo, not only because it meant a break from math, but also because working in Logo was a lot of fun, and it was easy. Unfortunately, that course was ‘squeezed out’ as far as my class was concerned by the pressure of our math courses over the next three years. During that time, however, the course had been rewritten using the programming language Scheme.

As a senior, I had a study hall period that I sometimes spent in my math classroom doing homework. It was on one of these days that I happened to overhear my math teachers talking about Scheme. I was already tearing my hair out in my Pascal class trying to learn something for the upcoming AP Computer Science exam – in fact, all I was learning was the page number of the reference section in our textbook, which I frequently consulted to see whether type declarations or variable declarations came first or to re-check how to declare a record for a linked list. Enticed by what I heard, I willingly gave up my study hall to come in four days of every week to learn Scheme on my own for no credit at all, using The Schemer’s Guide.* My reward was that I regained the enthusiasm and interest I thought I had lost six years earlier.

In the four months it took me to complete my course in Scheme, I learned more about computer programming than I had in my two years of Pascal. In less than five minutes after I began reading the text, almost everything I learned more than three years previously in our aborted Logo course came back to me. Five minutes, not the two days it took to recover from just one summer away from Pascal. There were hardly any rules of syntax to remember. Furthermore, throughout the entire four months, I never touched a computer. The ease of learning and using Scheme gave me such confidence in the programs I wrote that I didn’t feel the need for the security of a compiler to check my work.

Simple Language Makes Learning Complex Concepts Easier
The thing I liked most about taking this course in Scheme was that I knew that I was learning something. Every concept I had ever tried and failed to understand comprehensively in my Pascal class – searching and sorting procedures, recursion, processing binary trees – was made clear when I studied them in Scheme. These things occur so naturally in Scheme that I couldn’t help but understand. After mastering the concept, I could then go back into my Pascal class and easily master the code. The point here is that concepts like these are universal in computer science. After you understand them, then you can learn the rules of any language in order to encode them. But it doesn’t matter how well you have mastered the syntax of a language if you don’t understand the meaning of what you are typing or the reason why it works.

Recursion serves as a prime example. My understanding was very vague; I knew that something was done over and over again. But after seeing the first recursive program in the Scheme text, I understood what it was all about. When we took the test on recursion in AP CS, my whole class seemed to choke, with grades in the 60s and 70s, and the second highest score in the 80s. Thanks to my background in Scheme, I aced the test. I couldn’t quite believe it myself! For the first time, I fully realized that Scheme was not only easy to learn; it was also easy to learn from.

It is a myth to think that length and complexity make a program impressive – a prevalent idea among my AP classmates. Scheme code is clear and easy to understand. There is no need for pseudo-code. Thoughts go straight from your head to clear, simple code. The strange thing is that Pascal sets you up to fall into the trap of complexity and to disobey the laws of top-down design. As a procedural language, it enticed us into trying to do too much in one procedure simply because it could be done. With Scheme, I couldn’t write a function that had more than one purpose. It is as inherently top-down as it is inherently recursive.

Computer Programming Is Fun Again!
In my four months of studying Scheme, I not only covered and understood everything that had been presented in the AP Computer Science course, but went beyond that to study functional programming, data and functional abstraction, objected-oriented programming, and artificial intelligence. I still can’t believe all the amazing things I have learned in this short time. This is how I wanted to learn when I was in that BASIC class in sixth grade. I had to wait six years to do it, but it was well worth it.

I wrote this article because I don’t want another kid to have to go through the frustration that I did and not get anything out of it. I don’t want another kid’s enthusiasm snuffed out by a pile of library books. I want students who study computer science to be inspired to create their own game. Kids never liked rules anyway, and that’s all we are – kids.

*The Schemer’s Guide serves as the basis for IMACS‘ series of University Computer Science courses.

It’s winter at IMACS headquarters in South Florida. What does that mean? Sunshine. Temperature in the 70s and 80s. New Yorkers at the mall. Gotta love it! With the holidays around the corner, you might be wondering what to get for the math or science lover in your family. So we asked members of our IMACS family to share some of their favorite books or movies for our Winter 2011 Staff Picks list. Instructors Guy Barmoha, Frances Keiper and Jeff Piskun offered some terrific recommendations. If you’re still in need of ideas, check out more favorites from our Summer 2011 Staff Picks blog post.

Guy Barmoha, Senior IMACS Instructor

Guy has a BS in Mathematics from Florida State University and a Master of Science in Teaching Mathematics from Florida Atlantic University, where he continues to serve as a Teaching Assistant. He has been a part-time instructor with IMACS since 1995 and has taught all levels of our Mathematics Enrichment courses as well as the summer Logic Puzzles course, a Computer Enrichment course, and an Electronic course.

Guy is an award-winning teacher who taught middle school math for 11 years, including the Great Exploration in Mathematics gifted program. He received the prestigious Edyth May Sliffe Award for Excellence in Teaching in 1997. In 2001, he was a finalist for Broward County Teacher of the Year and was named Broward County Middle School Teacher of the Year in 2004. For the past four years, Guy has been a Mathematics Curriculum Specialist for Broward County Public Schools, and before that, he spent two years teaching math to distance-learning students. As you can tell, Guy is one busy, well, guy! But he always manages to find time to teach at IMACS. As he puts it, “Teaching here is always a bright spot in my week – the interactions with the students, parents, and staff always make it feel like home. Not to mention the great curriculum!”

Guy’s survey response is below:

“There are quite a few books that I enjoyed reading, not all related to mathematics. Even though we are mathematics educators, we all understand the importance of literacy. It is hard for me to pick a favorite book, so I will choose two to discuss. One that has some sentimental value, especially since we are discussing IMACS, is called What Is the Name of This Book? by Raymond Smullyan. This is more a compilation of logic puzzles than a novel; however, there are surely stories told within the book. You may ask why I chose this book. Well, the answer is simple – this is the book that reminds me of learning to teach at IMACS. In this book, students have to solve logic puzzles to find their way around the Island of Knights and Knaves, where Knights always tell the truth and Knaves always lie. Many of our logic puzzles that we use at IMACS are based on the problems in this book and other Raymond Smullyan books. I can still see our late founder, Burt Kaufman, teaching from this book and showing all the cases and subcases that students have to consider to solve the puzzles.

The second book is named Innumeracy by John Allen Paulos. Since we mentioned how important literacy is, we should not overlook the importance of numeracy. This book discusses consequences of innumeracy. A story from the book that sticks with me is the one about the stockbroker. The story goes something like this …

… Suppose I told you that I could predict the movement of the stock market correctly for the next five weeks in a row. Would you trust me enough to be one of my clients? Most people would. Well what you may not know is that I gave the same deal to 2,048 people. I then told half of them that the stock market will drop, and I told the other half that the stock market will rise. After the first week, there are 1,024 people who believe I predicted the movement of the market. Of those 1,024 people, I tell half that the market will drop and half that it will rise over the second week. By the end of this cycle, I will have 64 people who will believe that I am knowledgeable enough about the stock market to be able to predict its movement for five weeks in a row. …

This book was full of interesting situations like the one mentioned above. This is why I enjoyed reading it and refer to it often.”

Frances Keiper, IMACS Instructor

Frances has a BS in Mathematics from Stetson University and an MS in Applied Math from the University of Central Florida. She has been teaching part-time for IMACS since 2003 and previously taught math at Broward College. Frances worked for IBM Federal Systems Division at Cape Canaveral, Vandenberg AFB, and in Houston on Space Shuttle ground support software and on an upgrade to Mission Control flight information systems. She’s also had a few international assignments with IBM in Melbourne, Australia, where she created software and hardware upgrades for various banks, and in Kuala Lumpur, Malaysia, where she managed a project for the state-owned telephone company.

Frances’s survey response is below:

“I loved Dune by Frank Herbert – the book, not the movie. I got totally lost in the fantastic but somehow believable world Herbert created and just hated it when I finished the book. (I recommend skipping the sequel.) Herbert created a physical world full of sand containing creatures perfectly suited to that environment such as giant worms that travel rapidly over and through the sand. Then he populated the world with people who had their own elaborate social order and customs, again perfectly suited to that world but unlike anything we know on earth. The magic of the book is that it is so rich in detail and written so vividly that it becomes very real to the reader. You are drawn into this made-up universe. I don’t believe, even amidst the mountains of details regarding the physical and the social systems of Dune, that there is a single bit that is illogical. It all fits together so beautifully. You just have to believe.

For a more recent favorite, I really liked The Disappearing Spoon by Sam Kean. It’s full of quirky tales from the Periodic Table.

I loved the play Proof, which I saw at American Heritage Schools’ Mosaic Theater. And I liked the movie, too. It’s about a famous mathematician who is working incredibly hard to develop a proof, something that will be acclaimed the world over. He is an old man in the story and dies. His daughter, a mathematician in her own right, cares for him and grieves at his death. At first you’re not sure if the old mathematician was a genius or crazy. His behavior was bizarre. After a while, you’re convinced he was crazy.

Then a young math student shows up and trolls through the old man’s notebooks looking to find or maybe steal his brilliant but maybe non-existent proof. The twist toward the end is that the student finds the brilliant proof, but the person who developed it is the old mathematician’s daughter! I especially loved the fact that the hero is a FEMALE mathematician!

I almost never miss checking in to see what topics NPR’s Science Friday covered during it’s most recent broadcast. And I also really like an Australian call-in science show from Triple J Youth Radio. It’s called Dr. Karl. Dr. Karl himself is an enthusiastic and engaging science guy who can explain anything in simple terms and will readily admit that he’s not qualified to answer when he isn’t!”

Jeff Piskun, Senior IMACS Instructor

Jeff has a BS in Mathematics from Villanova University and an MS in Sports Administration from St. Thomas University. He started with IMACS in 2003 and is currently one of our part-time instructors. Jeff also teaches middle school math. A big sports enthusiast, he worked for over six years in sports and entertainment venue management for several professional teams, including the Florida Marlins, Miami Heat, and Florida Panthers.

Jeff’s survey response is below:

“Two books I would recommend are Freakonomics and Super Freakonomics by Steven Levitt and Stephen Dubner. These two economists use basic economic principals and basic statistics to look at real-life situations and investigate the hidden side of everything. The books are written in a fun but eye-opening manner and explain things like: why charging parents late pickup fees will actually increase late pickups not deter them; why your realtor actually does not have your best interest at heart; how walking drunk is more dangerous than driving drunk (not endorsed!); that many government programs actually have the opposite effect than intended (shocker). Parents should note that the books address some adult topics, so beware, but they are really an eye-opening read.

I enjoy movies that are similar to the original Stargate with Kurt Russell and James Spader. I like anything with codes and ancient secrets and the science/adventure/historical fiction genre overall. I’m intrigued by the idea that even though certain events are part of “history,” we still do not know everything about what occurred and why. Many many years later there are still mysteries and puzzles that need to be solved and theories to be investigated. Codes, puzzles, and mysteries based on historical events and real data are exponentially more fascinating than fictional ones.”

Guy, Frances and Jeff – Thank you for the awesome recommendations!

To our readers – Thank you for making our blog a part of your online experience. We sincerely appreciate your time, comments and feedback. Our next post on December 22nd will be a classic from the IMACS vault. All the best to you and your families for a wonderful holiday season and happy and healthy New Year!

Milo Gardner may be retired, but he’s not letting his mind rest idle. This amateur code breaker chatted with IMACS about his mathematics background and how it influenced his life. After serving in the United States Army as a cryptanalyst, Milo went on to earn his B.A. in Mathematics with a minor in History of Economic Thought at California State University – Chico. What followed was a career in aerospace engineering and an M.B.A. from CSU – Fullerton. Years later in retirement, Milo’s curious mind, a letter to the editor, and a meeting at a coffee shop led him to his current passion – decoding ancient Egyptian math texts. IMACS blog readers can review his extensive list of online publications on the subject. Now let’s hear from Milo in his own words.

Please tell us about your mathematics background, including what interested you as a child.

Baseball and sports of all types filled my youth. In the 8th grade I was sports editor of our school newspaper. This meant computing box scores and other game statistics for the various teams and writing up short narratives. Several sports teams were enjoyed during high school. Basketball was my favorite. Math was a special high school interest, as well as Spanish, chess and the sciences. Algebra I, Algebra II, Geometry and Trigonometry were studied in the context of set theory. That is, math students determined in advance which number system(s) would solve particular problems.

Right out of high school, the US Army was joined with hopes of spending time in Europe. My high school language skills were tested first. Two entrance exams for the Defense Language Institute at Presidio of Monterey, California, were taken. Luckily, the second exam score was low. The Army’s code-breaking tests followed, which were passed. In a five-month code breaking school, language and number-based patterns were studied. Techniques identified one-to-one, two-for-one, and other substitution systems. Finishing third in a class of 20, Germany was selected as my two-year assignment. Lower ranked students were sent to Africa, Turkey, Korea and Japan. In Germany, ad hoc Russian language projects were assigned to cryptanalyst and linguist teams. A two-month side trip to Lebanon widened my foreign language exposure to include Arabic.

Upon discharge from the Army, a number of my co-workers went to work for the National Security Agency (NSA) in Washington, D.C. I went to college in Northern California and earned a Mathematics degree with a minor in History of Economic Thought, with an intention of applying to the NSA. Computer programming courses were taken, as I was preparing to be a high school math teacher as a back-up career. Upon graduation, wishing to be married and raise a family, a southern California aerospace engineer accepted. The pay was better than teaching. Equally important the location kept me and my wife-to-be close to both of our families.

What kind of work did you do in the aerospace industry?

The first aerospace position was at Vandenberg AFB as a systems analyst. Western missile test range issues input computer-generated data to hand drafted range safety charts. The charts factored in daily wind measurements and drag aspects of missile parts that allowed three-second delays for the missile safety officer to blow up errant missiles. Nearby populations were protected. Subsequently, college programming skills were applied working with a team that automated the hand drafted charts.

The second aerospace job was at Rockwell International in Fullerton, California. Failure patterns of Minuteman I, II and other avionics guidance systems were studied in terms of maintainability issues. While at Rockwell, evening business classes were taken towards an MBA degree. Upon graduation, a career change allowed our family move to northern California to be near our respective families.

You raised a daughter who went on to become a civil engineer. What advice can you offer to parents of mathematically talented girls on how to nurture their talent?

Missy, my CE daughter, was self motivated by the second grade. All three of my children played musical instruments. Parental guidance consisted of coaching youth softball and baseball teams up to age 12 and supporting each child’s active social life. Thereafter, tryouts for competitive teams were arranged. Missy made a traveling team at age 14 in an organization that her older sister played. My wife and I attended most of Missy and her sister’s weekend tournaments. Our children knew their parents were their biggest supporters.

Missy was strong willed and stood up to basketball, softball and volleyball coaches in high school. Her sports experience gave her confidence to confront one engineering professor in college who refused to call on women in the class. After receiving a failing grade at mid-term, she called a conference with the professor and asked why he had not taken even a single question from one woman in the class. Her strong position was understood and respected. Thereafter, in-class questions were answered sufficiently for her and other women to earn passing grades. Today, she is an engineer working for a private firm. Incidentally, she told us this story weeks after the situation had occurred. Missy had the confidence to handle it herself.

In retirement, you now pursue code breaking as a hobby with a specialization in ancient Egyptian math texts. How did you become involved in these pursuits?

In 1962, an upper division college history of math class told a fuzzy history of zero story. Zero, as we know it today, did not reach Germany until 1200 AD, in time for the birth of our base 10 decimal system in 1585 AD (that defined n^0 = 1), an unbelievable assertion. “Some day I’ll research that topic,” I told myself. In 1988, six months were spent studying the topic at two local university libraries. Medieval and older Near East numeration systems including Classical Greeks used zero, a round figure topped by two dots in clear ways. Babylonians and Egyptians used zero as a limit 1,500-2,000 years earlier. Zero was also the value of empty sets in an Egyptian double entry accounting system. The older uses of zero did not use placeholders. Care had to be taken to read the context of mathematical documents and inventories –- issues that I knew well as a military code breaker.

After completing the study of the longer history of zero, an unexpected event took place. Acting on the dehumanization of classroom math topics (e.g., omitting personal stories like how the pre-teen Gauss summed the addition of 1 to 100 by a formula), I wrote a letter to the editor of the Sacramento Bee on the weaknesses of the 1990 California Math Framework. The day after the letter was published a phone call from a retired electrical engineer was received. Noel Braymer asked that we meet at local coffee shop. I said yes, and my retirement world changed for the better.

Noel had worked on 1650 BCE Egyptian text called the Rhind Mathematical Papyrus (RMP) for 15 years. A 50 member RMP 2/n table was encoded. The table took up 1/3 of a papyrus that contained 87 other problems. Noel offered a modern number theory solution to the 2/n table. Number theory stresses prime numbers in ways that ancient and modern mathematicians parse divisors of composite numbers into primes. The ancient 2/7 was recorded as 1/4 + 1/28. What set of ancient rules were used in the entire 2/n table?

The 2/n table encoded 2/3, 2/5, …, 2/101 to concise unit fraction series in ways that scholars hotly debated during the 20th century. Robin-Shute published the Rhind Mathematical Papyrus text in 1987 and suggested one incomplete solution. Noel gifted the book to me, and asked if I would assist in publishing his work. I said yes, provided the ancient scribal methods were also decoded and published.

Ten years later, working with a linguist, a sister document to the RMP, the Egyptian Mathematical Leather Roll (EMLR), was decoded with modern number theory. Attempting to explain connections between the two documents, aspects of the RMP 2/n table construction methods slowly emerged. Another seven years passed. Finally, by considering Egyptian wages paid in commodities, a 2011 paper included a complete solution to the 2/n table problem as an appendix.

In your opinion, what mix of interests and skills makes a person well suited for a career in cryptography? What should kids who are interested in code breaking be doing now to prepare themselves for a career in this field?

Students should enjoy solving all types of puzzles. I have loved crossword and other puzzles since high school. Learn a foreign language and learn about new and old foreign mathematical issues. Enjoy competitive individual and team games. Chess and bowling took up much of my free time. Choose your games and puzzles wisely. To pursue a puzzle solving career, a student should learn to contribute to all sorts of teams. Team membership is an important skill in many aspects of the adult world.

Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.

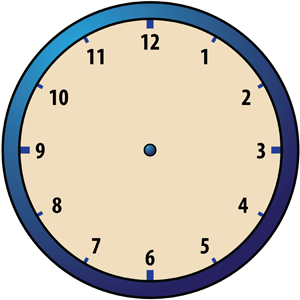
Consider a clock face such as the one shown below:

If the clock shows 10 o’clock, what time will it show 11 hours later? If the clock shows 5 o’clock, what time will it show 12 hours later? If the clock shows 6 o’clock, what time will it show 6 hours later? If you answered 9 o’clock, 5 o’clock and 12 o’clock, respectively, then you’d be right. This exercise suggests a new kind of arithmetic. Let’s call it “clock addition” or, because this kind of addition involves just the numbers 1 through 12, “Clock 12 addition” and denote it by +₁₂. Then the following statements correspond to the three questions above:

10 +₁₂ 11 = 9

5 +₁₂ 12 = 5

6 +₁₂ 6 = 12

Notice that the number 12 plays a very special role in Clock 12 addition. When you add 12 to any of the numbers from 1 to 12, the number remains unaffected. For example, 5 +₁₂ 12 = 5, 12 +₁₂ 12 = 12, etc.

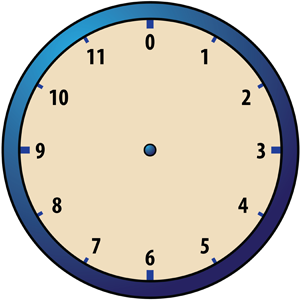
In ordinary addition the number 0 has this property. This suggests that it might be convenient to replace the “12” on our clock face by a “0” so that our clock face looks like this:

With this slight change from the usual clock face, we can now summarize the situation as follows: Clock 12 addition involves the twelve numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. We denote this set of the numbers by Z₁₂ (read, “Z sub 12”). Here is the rule for computing x +₁₂ y for any numbers x and y in Z₁₂.

For all numbers x and y in Z₁₂, x +₁₂ y is equal to:

x + y, if x + y is less than 12, or

x + y – 12, if x + y is greater than or equal to 12

In plain English, that means: To find the Clock 12 sum of x and y, first find the ordinary sum of x and y. If this ordinary sum is less than 12, you are finished – the Clock 12 sum is just the ordinary sum. On the other hand, if the ordinary sum is greater than or equal to 12, then subtract 12 from the ordinary sum to get the Clock 12 sum.

Notice that in any case, as long as x and y are in Z₁₂, x +₁₂ y will also be in Z₁₂. (Can you prove that?) Since for any numbers x and y in Z₁₂, the Clock 12 sum, x +₁₂ y, is again in Z₁₂, we call +₁₂ an “operation” on Z₁₂. Similarly, ordinary addition is an operation on the set of all natural numbers, N, which consists of the numbers 1, 2, 3, … . On the other hand, ordinary addition is not an operation on Z₁₂, and ordinary subtraction is not an operation on N. (What are some examples that support this statement?)

We have been calling +₁₂ “Clock 12 addition” because it’s very closely related to the kind of adding you do on a real clock. The operation +₁₂ is also called “addition modulo 12” or “addition mod 12” for short.

Clock 12 Addition Game

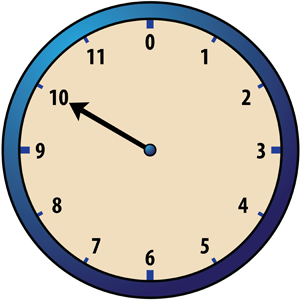
Now we’ll describe a game called “Clock 12” that two players, A and B, can play on a circular board. You’ll need a movable arrow for the hour hand so that your game board looks like the figure below.

Player A begins the game by placing a checker on one of the twelve numbers around the edge of the clock face. The hour hand is placed so that it points at the number on which the checker has been placed. The corresponding time is called “the hour.” For example, if Player A puts a checker on 10, the hour hand is placed so that it points at 10. Player A then says “The hour is 10 o’clock.”

Player B makes a move in two stages: first by placing a checker of a second color on one of the unoccupied numbers, and then by placing a second checker of the same color in such a way that the following is true: The starting hour plus (mod 12) the number of hours corresponding to Player B’s first checker is equal to the time corresponding to Player B’s second checker. The arrow is then made to point at the number on which Player B’s second checker was placed, thus indicating the new hour. Player B then declares the new hour.

Example 1
Suppose Player A begins the game by placing a checker on 10. Then the hour is 10 o’clock. If Player B chooses 4, then his or her first checker is placed on 4, and the second checker is placed on 2 because 10 +₁₂ 4 = 2. The hour hand is then moved to 2 o’clock.

Example 2
Suppose Player A chooses 0. If Player B chooses 4, the first checker is placed on 4. In this case, 0 +₁₂ 4 = 4, and Player B already has a checker on 4. Therefore, there is no need to place a second checker on 4, and so Player B’s turn ends with the hour being 4 o’clock.

Example 3
Suppose Player A chooses 10 and Player B chooses 0. Then, since 10 o’clock plus 0 hours is 10 o’clock, Player B’s second checker ought to be placed on 10. However, Player A’s checker is already on 10. In this situation, Player B takes Player A’s checker and replaces it with one of his or her own. The hour hand, which was pointing to 10 before Player B’s move began, will not be changed. The hour is still 10 o’clock.

The players continue to alternate turns using rules described in the examples above. If, after completing his or her turn, a player leaves the board so that there are no more unoccupied numbers, then the game is over and the player with the most checkers on the clock wins!

The benefits of math competitions are well known: focusing on goals, dealing with pressure, learning teamwork, and building friendships are among those typically mentioned. Math competitions also allow for the much needed celebration of intellectual achievement the way athletic achievement has always been celebrated. At IMACS, many of our math enrichment students enjoy competing in the American Mathematics Competitions, International Mathematical Olympiad, and MATHCOUNTS among other contests, so we have a very positive view of math competitions, particularly for the kids who thrive in that environment. We’re extremely proud of our numerous students over the years who have performed well in these prestigious contests. We’re equally proud of our numerous students over the years who have thrived in quiet contemplation.

This brings to mind an article published last week by The Wall Street Journal on the challenges encountered by Type A parents raising Type B kids. The article talked about different ways that ambitious, competitive, and hard-driving parents modify their interactions with or expectations of their dreamy, mellow, and seemingly laid-back children to foster healthy parent-child relationships. Whether Type A or not, most parents are cognizant of today’s ultra-competitive global environment, and many feel a sense of urgency to nudge, push, or even pressure their kids to achieve. It’s not a stretch to imagine the parents of a mathematically talented child thinking, “If all the other kids are involved in math and science, then my child should be doing even more.” Here’s the thing: What makes an activity suitable for even more depends on what works for your child and is not necessarily the same activity enjoyed by all the other kids but with more time dedicated to it or with better results.

For parents considering activities for their mathematically talented child, it is important to understand how innate personality factors into the mix that determines whether math contests provide a net positive experience for that child. Just as there are natural-born competitors among mathematically talented students, there are also natural-born dreamers. These kids used to get a bad rap for being unfocused, undisciplined, and even lazy. There was no observable productivity associated with daydreaming so, of course, it had to be a waste of time. Not so fast. In 2009, researchers from the University of British Columbia published a study in the Proceedings of the National Academy of Sciences detailing that brain activity increases when our minds wander. Reporting on this finding, ScienceDaily.com put it well: “[B]rain areas associated with complex problem-solving – previously thought to go dormant when we daydream – are in fact highly active during these episodes.” And from The Wall Street Journal: “These sudden insights … are the culmination of an intense and complex series of brain states that require more neural resources than methodical reasoning.”

If your child is more of a dreamer (or just not drawn to competition), activities that would cultivate his or her talent in and appreciation for mathematics may differ from what is offered through a typical regional, national, or international math contest. Students of this personality type often find more success and satisfaction with math enrichment programs that focus on deep problem-solving over computational prowess. This is not to say that your child shouldn’t at least try participating in some type of competitive math. The experience just might open up a different side of his or her mathematical personality. In fact, our math enrichment classes use game-playing and mini-competitions as teaching tools, and most of our students really enjoy this aspect of the class the best. But if it’s clear that competition does not bring out the best in your child, we encourage you to explore other options including letting your child have more free and unstructured time to let his or her mind ruminate about the wonders of mathematics.

For parents of talented children, the secrets of mathematical success are really not that different from general advice on positive parenting. They include understanding what kind of child you have, knowing what motivates him or her, and fostering an environment that includes the kind of math activities or, quite possibly, freedom from structured activities that align best with that motivation. And if having a dreamer for a child still makes you worry, just think about the great mathematical and scientific discoveries we owe to dreamers of the past. You never know what grand ideas are simmering behind those eyes staring off into the distance.

Dreamer Matching Puzzle
We made a simple matching game out of the Wall Street Journal article that reported on the aforementioned University of British Columbia study. See if you or your kids can match the great thinker with his profound idea and what he was reportedly doing at the time moment of insight. Answers may be found in the article.

Great Thinker: (A) Archimedes, (B) Newton, (C) Einstein, (D) Descartes, and (E) Tesla.

Profound Idea: (1) special relativity, (2) coordinate geometry, (3) alternating electrical currents, (4) calculating the volume of an irregularly shaped object, and (5) law of universal gravitation.

Dreamy Activity: (i) lying in bed watching flies on the ceiling, (ii) taking a bath, (iii) watching an apple fall from a tree in an orchard, (iv) taking a walk, and (v) imagining trains and lightening.

Editor’s note: Regular readers of this blog will notice a slight change going forward. IMACS will be switching to a bi-weekly publishing schedule with our next post appearing on November 10, 2011.

My earliest memory of chess was from when I was around three years old. I remember sitting on the edge of a rug playing with colorful LEGO blocks. When I looked up, I saw my father and my oldest brother playing chess. The board was illuminated so brightly that it looked as if the pieces were shining. I looked back down at my blocks, and they seemed so boring compared to the multitude of pieces and squares and interesting stuff happening on the board above. That was when I was first aware of my desire to play on that board and with those pieces. I would crawl over to where my father and brother were playing, take a few game pieces, and put them on the board too. After “playing” with them a few times in this way, I was henceforth banished from the vicinity of their games. This continued for two years until my mother determined that I had the capacity to understand what was going on. However, nobody believed her, so she taught me the basics herself. It took me about a week to grasp those rudiments of chess, after which I was handed over to my father for further instruction.

My father and I would take a chess set and chess book from our library at home and bike to one of our favorite places. There, my father would set up a position from the book on the board, and we would puzzle it out together. In the beginning, we would actually move the pieces, but after a few weeks my father urged me to work out the entire solution and move the pieces only in my head. We studied tactics, strategy, endgames, etc. I gradually improved to a stage where I could have a “reasonable” game with him (“reasonable” in the sense that I wasn’t losing after the fourth move). A few years later, when I was eight or so, I learned that there was a chess club at a local elementary school, so naturally I went to check it out. There I found good competition with kids my age and with one boy in particular. We were about evenly matched, so when he went to a tournament and won a big trophy, I wanted one too! That’s how I got started with tournaments.

For a few years though, competition took a back seat to other important family events, which had the strange habit of conflicting with tournament schedules. School was also a factor: It would have been difficult to actively study chess and play in tournaments given all the classwork and homework I would have had to make up for the days I missed. Also, tournaments usually run through Sunday, and my Sundays were taken up with IMACS. I loved IMACS so much that I wasn’t willing to skip even one class if I could help it. When I was in third grade, my parents withdrew me from the school I was attending for a variety of reasons, including lack of a challenging curriculum that kept me perpetually bored even though I skipped a grade. I was homeschooled while my parents searched for another school, and I recognized this as an excellent opportunity to have a say in my education. I was on my best behavior for months before I convinced my parents to homeschool me forever! Now that I was homeschooled, I had loads of free time. Also, my IMACS classes were moved to Thursday. So, now that I had the time and was not sacrificing IMACS, I got interested in competitive chess again.

From my friends at tournaments, I found out about the Internet Chess Club (ICC). With my new ICC membership, I played for hours after my studies were done (which at 3rd grade took a grand total of an hour and a half). My parents always encouraged me to play up (i.e., at a higher level), so already in elementary school I was regularly playing up in K-12 events. This wasn’t very good for my rating as I usually lost many games, but as a consolation, from age 8 on, I was Florida’s Top Girl at the K-12 level for several years in a row. At that time, Women’s World Champion Grandmaster, Alexandra Kosteniuk, was handing out the Florida’s Top Girls prize. After a few years of shaking hands with her, my mom asked her to coach me. I improved dramatically under Alexandra’s guidance – I developed an opening repertoire, whereas before I usually made up my own openings (that sometimes didn’t turn out well). As my rating shot up, I made the Susan Polgar’s National Team for Girls and was invited as the representative from Florida to play in her 2009 National Invitational for Girls event. That was my introduction to girls-only events. I took second place, and made new friends. My mom is always checking the Web site for FIDE (the World Chess Federation, or Federation Internationale des Echecs). There she found out about the 2010 North American Youth tournament. The fact that one of my new friends was going to attend helped seal the deal. We were both US representatives, and it felt awesome to tell people that I was representing the United States of America. A series of wins and draws took me to the final round where I ultimately won! And so in my first international tournament I got my first gold medal for the US. As I hadn’t been having great results before that tournament, the win was welcome and kept me studying chess even with my increasing workload. (Studies at my age now aren’t as easy as in 3rd grade!)

My coach, Alexandra, started a family, which meant that she rarely traveled from her home in Russia to the US anymore. Thus, my parents decided to choose a different coach to fill in the gaps – four-time US Champion and Grandmaster Alexander Shabalov. Under his guidance I won the 2011 US Girls Junior (U21) Chess Championship this past August with an undefeated score. Whenever I’m feeling low, there always comes a win to keep me motivated. Chess is an amazing game, and I’m very competitive, so that also always brings me back to competitions. I love playing and seeing how I stand against some of the big names in chess (or more often, those who say they’ve played them). My favorite competitions are the one day tournaments, because I get to go home quickly. The longer 6-7 day tournaments, like the Susan Polgar, North American Youth, and the US Junior Girls leave me homesick toward the end. (For how long can one eat hotel food?) Now I’m in a lull between tournaments, so I practice by playing on ICC and chesscube.com for about an hour each day. My next big tournament will be the World Youth Chess Championship in Caldas Novas, Brazil, this November where I will represent the United States.

Dan Dugger is a professor in the Department of Mathematics at the University of Oregon. He received his Ph.D. in mathematics from the Massachusetts Institute of Technology and his B.A. in mathematics from the University of Michigan. Professor Dugger is a graduate of Project MEGSSS of Broward County, Florida, which used the mathematics textbooks that underlie the EMF Math online program. As a high school senior, he submitted an original research paper entitled "On the Homomorphisms between Finite Abelian Groups" to the 41st International Science and Engineering Fair, winning–among several other honors–the first place award from the American Mathematical Society.

When did you know that you wanted to be a mathematician? Who or what experiences influenced you in that direction?

When I was in elementary school, there was a class for gifted students run by a remarkable teacher. Her idea was that the students should be in charge of their own education, so she had them each pick a subject they wanted to study. At first I studied space exploration, and then I studied whales. The next year I studied computers for a long while (this was in the days before anyone had a computer in their home!), and the year after that I switched to lasers. One day I was reading an explanation of lasers in a physics book when an older kid came along and in a tone of complete awe asked, "Danny, you're studying physics?" I sheepishly explained otherwise, and he went about his business, but I came away with the idea that physics was a difficult and impressive subject! So the next year, in fifth grade, I was determined to study physics. After that, I was convinced I wanted to go to Caltech and become a physicist.

At that point, I honestly had no idea that there were such things as mathematicians. I liked math, and I liked it when my dad showed me mathematical things he knew that were over my head, but I had no idea a person could make a career of it. Then in middle school I went into Project MEGSSS (the precursor to IMACS) and started learning from the Elements of Mathematics curriculum (the basis for the EMF curriculum). At that point I felt the wonderful beauty and poetry in mathematics. I had great teachers like Burt Kaufman and Ed Martin who were encouraging and really made this material accessible, and thanks to them I was hooked. So pretty much from then on I wanted to be a mathematician.

The important point that I want to get across is this: I remember fairly little of elementary school, but I remember every subject I studied in the four years of that gifted class. That strikes me as remarkable. And in a very direct way I see that class as having put me on a path that led me to my eventual career. It's really hard to overestimate the effect that good, caring teachers have on children.

You attended the University of Michigan at Ann Arbor for your undergraduate degree. At what point did you start looking into grad schools? What were you looking for, and how did you decide on MIT?

As an undergraduate, there were times when I was uncertain that I still wanted to go to graduate school, but I also didn't know what I wanted to do. A kind math professor grabbed me one day after I had taken his class and said "Are you planning to go to graduate school? Because you really should!" At his suggestion I participated in a summer research program at Michigan with another great professor. The next fall this professor sat me down and said, "Okay, here are the places you should apply to graduate school: Harvard, MIT, Princeton…" I was pretty shocked! I had no idea I would be able to get into schools like that.

So I applied for graduate school, although I was still not exactly sure that this was what I wanted to do. For a while I was convinced that I wanted to go to University of Chicago, but when I visited there, it didn't quite click for me. I remember quickly calling up MIT afterwards and asking to arrange a visit! Luckily, during that visit something did click. What I mostly remember was the very pleasant atmosphere among the graduate students at MIT. Seven or eight of them took me out to dinner, and I remember they spent the whole evening gossiping about the professors in the department. That doesn't sound like a good reason to choose a graduate school, but somehow it worked.

I think the real lesson here is that visiting schools is very important. It is quite difficult to know, or to predict, when things are going to click or not click. Every school is different, and different things work for different students.

Tell us about your years at MIT. How did you choose your advisor, or is it the advisor who chooses the student? How do you decide on the topic for your thesis?

I came to MIT determined to study a subject called commutative algebra. But once I was there, I found myself more and more in the company of topologists. There weren't many people studying commutative algebra at MIT, but there were numerous topologists–it was a very active and exciting community. My best friend was a topology student, and I always seemed to be hanging around the topologists and their interesting seminars, so at some point it seemed that I should just become one of them!

Unbeknownst to me at the time, other forces were also at work. During my first semester at MIT I took a seminar in topology run by a retired professor, and he decided that I should become a topologist. (He didn't tell me this at the time.) He somehow set things up so that I started talking regularly with a brilliant topologist named Mike Hopkins, and after a while Mike became my advisor. I never formally asked him to be my advisor, and he never formally invited me to be his student; it somehow just came to be. However, this is somewhat atypical. Most students just choose someone who is in the area in which they want to work, possibly having already taken a class from such a person, and simply ask. It's typical for the student to do some independent reading under the professor's guidance to see if things are a good fit before anything is set in stone.

Concerning choosing a thesis problem, most advisors will assign the student a problem based on the student's interests. Usually it is a problem the advisor has some ideas about, so that he can suggest a plan of attack. Some advisors, however, have the students find their own thesis problem. In some ways the latter is a better, albeit more challenging, technique because eventually in his or her career a student will have to learn to do this anyway. In my own case it was somewhere in between these extremes, but closer to the latter.

Were there challenging times when you just hit a wall with the research? How did you keep yourself motivated?

It is not just that sometimes there is a wall to get past; it would be fair to say that almost all of the graduate school experience is a wall. Let me try to explain. Everyone goes into graduate school assuming that when they write their thesis it's going to be fun and beautiful like the mathematics they fell in love with, but that is an idealized view. When you take mathematics courses as an undergraduate, you are presented with a very beautiful, developed theory. But it's important to realize that what you are seeing in these courses has been refined over hundreds of years–you are almost never seeing "raw mathematics" as it comes out of the ground, so to speak. Instead of polishing a beautiful diamond, a working mathematician spends most of his or her time digging in a mine, carving away at the rock. In addition, when you learn mathematics in a course you are carefully protected from all the false trails that mathematicians took to get there. Actual mathematics research has many false trails, or trails that lead a little ways but then peter out. Someone once described their life as a mathematician this way: "I spend my days writing lots of stuff on the blackboard, most of which turns out to be wrong." This description, although exaggerated for a humorous effect, is not that far off.

So in some sense graduate school ends up being largely about making a transition in how you see mathematics. It is not easy to do. And a challenging factor that accompanies this is that the gulf between working mathematicians and students becomes particularly large here. Working mathematicians made this transition long ago in their careers, and many are not quite aware of it anymore. This can make communication between students and their professors somewhat frustrating.

The question of how to keep motivated in the face of all this is the crucial one. It is very difficult, and that difficulty never goes away. Not many people get PhDs in mathematics, and far fewer are still engaged in research ten years afterwards–and I think this is largely because of the motivation issue.

I don't want to give the impression that this is an impossibly difficult career path; obviously, there are new math PhDs awarded every year. I do think it is important to understand that life as a mathematician is very different from life as a mathematics student. When you are a student doing exercises from a book, the distance between what you know and what you are trying to find out is relatively small. In mathematics research, that gap is multiplied by a hundred. It can seem like you are walking from San Francisco to New York, but with the added twist that there are no roads or maps and that you don't really know that New York is even there! Everyone has to find their own answers for how to keep motivated on a journey like that. You can look at it as an insurmountable feat, or you can look at it as an challenging adventure, or somewhere in between. For what it's worth, I will tell you the answers that have worked for me. For myself, it always comes back to the fact that I like teaching; I like understanding neat things and sharing them with people. This is where my motivation comes from, even for my research. I'm always out to find that next "neat thing" to explain.

How did you know when you were ready for your thesis defense, and what was that like?

In most U.S. mathematics departments the thesis defense is, to some extent, a formality. Basically, you are ready when you have proven a new theorem. As long as you can convince three or four professors that it really is a new theorem, and that your proof is correct, you will get your PhD. The defense consists of you giving a lecture about the topic and about what you've done, and as long as you can do this intelligently and answer a few of the professors' questions, you get your PhD.

In my case, I was ready for my defense much earlier than I realized at the time. I had a new result that would have made a perfectly fine thesis, but it wasn't the result I was after—it wasn't the kind of result I wanted my thesis to be about. But looking back, having seen much more of the mathematical world since then, I realize this was pretty silly. I ended up spending about eight more months working on it until I got a result that I was happier with in the end (although still not really the one I wanted!). It wasn't really wasted effort, but it also wasn't necessary to put myself through the extra struggle.

So you officially become Dan Dugger, PhD. What's next in the process?

This is an important question. The first thing you need to realize is that getting a PhD is just the beginning. Someone once described it to me as a "license to practice mathematics." Getting your license doesn't mean you're ready for the Indy 500, or even rush hour on I-95. In mathematics, recent PhDs do not immediately go on to become full colleagues in a math department somewhere. Usually there is an apprenticeship process called a post-doctoral position that lasts two to three years, and, depending on circumstances, a person might end up doing more than one of these. (I did two of them for a total of five years.) During these years a person needs to establish his or her own research program and prove (by writing several papers) that he or she can do research without having an advisor. Assuming you do this, you can get a tenure-track position in a research department. These are highly competitive jobs, so you go where you are lucky enough to get an offer.

And what interesting research are you working on now?

I'm afraid this would take a very long time to explain. It is the curse of being a mathematician: it is very hard to explain your work to people outside the field, in a short amount of time and space.

“Indeed, your conception of failure might not be too far from the average person’s idea of success, so high have you already flown.”
– JK Rowling, Harvard commencement speech, June 2008

“People who have an easy time of things, who get 800s on their SAT’s, I worry that those people get feedback that everything they’re doing is great. And I think as a result, we are actually setting them up for long-term failure.”
– Dominic Randolph, Headmaster, Riverdale Country School, New York Times Magazine, September 14, 2011

Two weeks ago, the science world was abuzz with talk of a report that neutrinos seemed to have traveled faster than light. News of this finding traveled pretty quickly as well, as media outfits worldwide ran headlines that (gasp!) Einstein may have been wrong. News like this would have been dismissed summarily were it not for the fact that the research team involved in this experiment are not exactly a bunch of weekend armchair physicists. They are part of the OPERA Collaboration working at CERN.

So why would these esteemed scientists put themselves out there to be met by the inevitable wave of skepticism, even ridicule? Because they understand that if they made an error, opening their research to scrutiny in order to find and correct the mistake is exactly what will help them advance their work and the work of others. In fact, the official press release announcing these unexpected observations quotes CERN Research Director Sergio Bertolucci as saying, “When an experiment finds an apparently unbelievable result and can find no artefact [sic] of the measurement to account for it, it’s normal procedure to invite broader scrutiny, and this is exactly what the OPERA collaboration is doing, it’s good scientific practice.”

At IMACS, we couldn’t agree more, and would further assert that the same principle applies in mathematics and computer science. Learning to fail well in these subjects is particularly important because of their exacting and objective nature. Your proof is logically consistent or it isn’t. Your computer program compiles or it doesn’t. There is generally no interpretive latitude around whether you’re right or wrong. There is no arguing that the instructor’s subjective judgment based on his or her personal ideology caused your poor grade. Add to that the tendency of talented students to have a strong aversion to failure and you can see that how resilient one is in the face of failure will be a major factor in determining how much success one has going forward.

While we’re not experts in educational psychology at IMACS, we’ve taught thousands of talented children over the years and are parents ourselves, and what we observe is that learning to fail well is a “scaffolding” process. A talented child who is allowed to have small failures early on without harsh consequences and who is involved meaningfully in determining and executing corrective action shows greater resiliency when faced with the next level of failure. This process builds on itself as the child grows older and the circumstances and consequences become more serious. The failures may grow, but so does the child’s ability and confidence to handle them effectively and independently.

So parental readers, take a look at your mathematically or scientifically talented, award-winning, perfect-scoring children and ask yourself, at this age when the consequences of failure are not so great, are they developing the resiliency that will allow them to take the intellectual risks that are necessary for great success but may also lead to major failure? Do they know from experience, not from having you tell them, that they have it in themselves to bounce back? Ask of yourself, do I allow my child to feel safe about having small failures now so that he or she can rise up from a bigger failure later when I’m not always going to be there to pick up the pieces? If not, then perhaps it is time to lead by example and show that you can make adjustments with an eye toward the long term. After all, if your child is someday going to make the next groundbreaking discovery in physics, he or she should get a head start by learning to fail well now.

Robots, robots, everywhere! If you follow current news on science or technology like we do at IMACS, then you’re bound to have noticed that robots are a popular topic. From the Roomba vacuum to the da Vinci Surgical System, these mechanical marvels affect many aspects our daily lives from the mundane to the life changing. Along the way, numerous robotics programs for school-aged children in the US and around the world have been established, and earlier this year the Boy Scouts of America introduced its new robotics merit badge.

Why the burst of interest over the past five or so years? Here are a few key factors that have recently come together to foster this growth: (1) The global economic downturn put a spotlight on which types of job skills are in demand and will be even more in demand in the future; (2) Industry and political leaders regularly note the gap between those job skills and the current levels of student participation and achievement in science, technology, engineering and math (STEM); (3) Robotics technology has become more affordable and accessible with companies such as LEGO developing robot kits that, while targeted toward children, enable the exploration of complex engineering and computer programming challenges; and (4) Education leaders recognize that robots could be used to engage children in fun and interesting activities that would deepen their understanding of all STEM subjects, along with teaching some important life skills.

There are at least two types of robotics programs: those that integrate robotics as part of a course curriculum and do not lead to a competition, and those that are organized as extracurricular activities and do lead to some type of competition. In a typical competition-based robotics program, each team of students is responsible for designing, building, and programming an autonomous robot to accomplish a set of pre-defined engineering challenges. The autonomous nature of the robots requires students to know or learn how to program them using a computer programming language. Some programs have separate showcases or entertainment-based categories that emphasize imagination and creativity. Most stress the importance of some kind of life skill, from simple teamwork all the way up through a whole menu of real-world skills that form a key part of the judging criteria.

Whatever kind of emphasis you’re seeking, there is likely to be a robotics program out there to match. If you’re just starting to explore options for competition-based programs, here is helpful list of national organizations to start with:

FIRST
• Founded in 1989 by the inventor of the Segway Personal Transporter.
• Over 2,000 teams from across the US and from 11 countries participated in 2011.
• There are four main divisions: FIRST Robotics Competition (FRC) is the flagship program for high school students. FIRST Tech Challenge (FTC) uses a head-to-head sports tournament model and is also for high school students. FIRST LEGO League (FLL) is for ages 9-14. Jr. FIRST LEGO League (Jr. FLL) is for ages 6-9.
• Rookie team registration for one FRC event and the kit of parts costs $6,500. Teams may register for additional events at $4,000 each, and they may spend up to $3,500 on additional parts for their robot. The FRC Handbook provides a sample budget for a rookie team attending one local regional event that totals almost $13,000, and that does not include any travel costs. If you had high hopes for your child competing in FRC but were not aware of the magnitude of the cost, don’t pass out just yet—finding sponsors is actually an integral lesson of the competition, as much as securing funding is part of research and development in the real world. The FTC program requires a much smaller investment, but one that is still in the range of $1,500 to the low thousands. At the other end, registration for Jr. FLL is $25 and the base kit costs about $140.
• Students may only use the official robot kits and other materials that are tightly prescribed in the program rules.
• While engineering is the heart of these competition, FIRST programs are equally designed to develop people and life skills such as time management, collaboration, communication, self-confidence, and leadership.

BEST Robotics
• Founded in 1993 by Texas Instruments.
• In 2010, over 850 middle and high schools participated. They are primarily based in Texas and surrounding states and in the Southeast.
• For the robotics game, teams compete four-at-a-time in round-robin matches. All teams must submit a project notebook describing their engineering design process. Students have the option of competing for an overall award that covers qualitative factors such as oral presentation, an educational exhibit, the engineering notebook, and spirit and sportsmanship in addition to robot performance.
• Participation for schools is free. There is no registration fee, and all materials are supplied at no charge. How can this program be free? Corporate sponsors provide all of the high tech equipment, which must be returned each year, as well as the software. The set of consumable materials is fairly simple and includes basic items such as plywood, PVC pipe, wire, screws, and tape. Creativity and inventiveness are essential qualities in this program.
• Participants are required to use the control system kits currently provided by corporate sponsor VEX Robotics (discussed below).
• BEST describes itself as being less about building robots and more about teaching students how to analyze and solve problems.

Botball
• Established in 1997 by the KISS Institute for Practical Robotics.
• Over 300 teams participated in 2011, including teams from Qatar. US teams are primarily from the West, Northeast, Texas/Oklahoma, Greater D.C. Area, and Great St. Louis area.
• The program is for middle and high school students. All teams, regardless of the ages of the students, participate in the same competitions.
• Teams compete unopposed in seeding rounds followed by head-to-head double elimination rounds. Those who are eliminated have the opportunity to be paired in cooperative alliance matches. All teams must also document their engineering process and present this work as part of the tournament competition. Students who prefer a non-competitive platform may submit an autonomous robot project, including robots integrated into artwork, to the showcase. Students may also submit short papers on specific robotics-related topics.
• For the 2012 season, the subsidized registration fee for US teams of $2,500 covers tournament participation, the Botball robotics kit, and programming software. The unsubsidized fee is $3,200. Reusing equipment from prior seasons reduces the registration fee by $530. Teams are encouraged to find corporate sponsors and to host fundraisers to defray costs.
• Students must use the official robotics kit, which includes an iRobot Create robot base, various additional parts, and all necessary tools to build the robot. The required programming language is KISS C, which was designed by the organizing sponsor for teaching robotics.
• One of the factors that Botball tries to differentiate itself with is the support it gives to educators. Every Botball region hosts a hands-on professional development workshop for team leaders, and the reusable equipment remains with them after the tournaments for use in the classroom.

RoboCup Junior
• Started in 1998 by RoboCup, an international organization whose purpose is to foster artificial intelligence and robotics research.
• In 2011, 251 teams from 29 countries participated in this predominantly international competition.
• The program targets students aged 19 or younger. While no minimum age is specified, students must be able to read, as well as write computer programs for their robots without substantial help from adults. Age divisions are broken into teams where all students are 14 and under, and teams where any student is over 14.
• There are three competition categories: soccer, rescue, and dance. The soccer challenge pits 2-on-2 teams of autonomous robots against each other. In the rescue challenge, robots must quickly identify victims within a simulated disaster scenario. The dance challenge is further divided into dance and theatrical performance and is designed to encourage creativity.
• Students may choose which robot platform and programming language to use, and they may also add additional equipment to the platform.
• RoboCup Junior differentiates itself by keeping the challenges the same from one year to the next. This point of this approach is to allow students to learn from their prior experiences and improve their algorithms and hardware as they grow.

Robofest
• Established in 2000 by Lawrence Technical University in Michgan.
• Almost 500 teams from the US, Canada, China, Korea, and Singapore participated in the 2010-2011 season. Nearly half of the students were from Michigan.
• The program has a division for students in grades 5-8 and one for high school students.
• Competition styles can be generalized into two categories: games that use fixed rules and open-ended exhibition. The game challenge changes each year. The exhibition category is designed to encourage creativity and includes a robot fashion and dance show and a robot parade.
• Registration is $50 per team, and some site hosts may charge an additional fee of the same order. Suggested robot kits cost about $200-250, and a playing field costs about $50.
• Students may choose any type of robot technology and programming language, as well as use tape, glue, bolts, nuts, etc. to construct their robots. Components and materials used to build robots and playing fields may be reused from year to year, thereby reducing cost.
• The focus is firmly on learning computer programming. Additional activities like giving a presentation on the team’s research findings are not included.

RoboGames
• Founded in 2004 by the president of the Robotics Society of America.
• At RoboGames 2011, 239 teams from 17 countries participated.
• All ages are welcome, so many teams consist of adults. Junior League events are restricted to participants aged 18 and under.
• RoboGames is more a collection of over 50 smaller competitions all happening in the same place over several days. This explains why it is promoted as the “Olympics of robots.” In fact, most of the events are sports-based. The Junior League does have more engineering-based events, as well as creative showcase events.
• The registration fee for most events is $50, but none costs over $250. Participation in many of the Junior League engineering events is free. The cost of equipment varies by event.
• Each event has its own rules for building and controlling the robot. For example, the LEGO-based competitions require LEGO parts, but other events leave the choice up to the participant. Some contests allow for remote-controlled robots, so those particular events would obviously not stress computer programming skills.
• The main goal of RoboGames is to encourage robot builders to expand outside their area of specialization as a way of fostering a cross-pollination of ideas.

VEX Robotics Competition
• Established in 2008 by Innovation First, the maker of HEXBUGs and owner of the VEX Robotics brand name.
• More than 3,500 teams from 20 countries participate in over 250 tournaments worldwide.
• The program is for middle and high school students, although a college-level challenge was recently added.
• In tournament matches, two alliances composed of two teams each compete against one another. Each match has a period where robots are controlled autonomously and a period where they are remotely operated.
• The registration fee for each team is $75. Robot starter bundles from VEX cost $300 for the simplest version and can go well above $550 for the most sophisticated model. The competition field and perimeter kits sold by VEX total $1,600, but the company also offers tips on how to build low-cost options. Total competition costs can definitely breach the $2,000 mark.
• As you might guess, teams are required to use the VEX Robotics platform.
• VEX bills its competition as “the fastest growing robotics program and largest middle and high school competition in the world.”

For additional information and resources on robotics as an educational tool, check out the following organizations:

Carnegie Mellon Robotics Academy – The academy is part of the university’s world-renowned Robotics Institute. Their mission is to use the motivational effects of robotics to excite students about science and technology.

NASA Robotics Alliance Project – The project’s mission is to create a human, technical, and programmatic resource of robotics capabilities to enable the implementation of future robotic space exploration missions.

Adam Sternberg began his path to engineering as part of Project MEGSSS in Broward County, Florida. (The principal curriculum developers and teachers for the Florida MEGSSS program founded IMACS in 1993 using the same Elements of Mathematics courses.) He went on to earn his B.S. in Electrical Engineering from the University of Maryland College Park and his M.S. in Electrical Engineering with a concentration in Digital Signal Processing from Florida Atlantic University. In his role as a software engineer for innovative companies such as AlliedSignal (now Honeywell) and RadiSys, Adam was responsible for developing software used with flight navigation tools and telecommunications products. He is currently a senior software engineer at Pace Americas. In his spare time, Adam has even been a volunteer teacher, sharing his knowledge of computer programming and university-level logic with elementary school students.

You were part of the first group of students in the Broward County MEGSSS program. What were your thoughts when you started progressing through the curriculum?

The MEGSSS curriculum (which has now evolved into the IMACS curriculum) was different from anything I had seen previously. In the standard honors math class, my friends were mainly doing more of the same material as the regular class at a faster pace. In MEGSSS, we covered the expected topics, but the majority of the time was spent learning concepts that students usually don’t see until college. In most math classes, theorems are stated as fact, and then students are expected to apply them. In MEGSSS, learning how to prove those theorems from principles proven earlier was an essential part of our education and resulted in us having a deep understanding and appreciation of the subject.

What knowledge and perspective did you gain during that time that influenced the career path that you took?

The subject matter from MEGSSS that helped the most was logic (predicate calculus). I found I always had an affinity with logic and the structure of proofs, and that made me comfortable with the process of coding in a high-level language, such as C or Perl. The MEGSSS/IMACS experience in general, with its emphasis on logical proofs building on previous theorems and axioms to explore new topics, evolved into an ordered approach to problem-solving that is the hallmark of a good engineer of any discipline.

Please describe what a software engineer does, big picture and day-to-day.

A software engineer is responsible for the design, implementation, and maintenance of a software product, whether it be a Web site, an app for a smartphone, or the radar on an airplane. This includes designing proper test cases for the product, and identifying and correcting bugs found in the product code. Software engineers are also often called on to make judgment calls in triaging bugs found during a test cycle and determining both the severity and the likelihood of a bug appearing in the field with a released product. As software and the equipment they run on are rapidly evolving, software engineers must also make sure that they are familiar with the latest trends in programming languages, algorithms, tools, and related technology.

In your experience, what kind of personality and/or non-technical skills makes a person well-suited to be a software engineer?

Good communication skills are vital to be able to explain technical details to a non-technical audience (such as customers or the sales team) because software engineers often work in a corporation and not a vacuum. Also, good detective skills (such as observing behavioral patterns) are vital to finding bugs. Finally, no one’s code is perfect, and colleagues and supervisors will find fault with an engineer’s design or code in a review, so a thick skin is also helpful.

What education, skills and training make for success in the job?

A Bachelor’s degree in Computer Science, Computer Engineering, or related field (such as Electrical Engineering) is vital, and a Master’s Degree is often preferred. As an engineer’s career progresses, tasks may become more senior in nature, so leadership, project management, and even mentoring skills are good to have. Structured problem-solving skills, like what students develop at IMACS, and solid design skills are vital.