• Information for Parents
• Information for Students
• Information for Educators

“In an online world, colleges have to think hard about how they are going to take communication, which comes over the Web, and turn it into learning, which is a complex social and emotional process.”
-David Brooks, New York Times, May 3, 2012

Over the last 15 years, the advances in our ability to share information broadly and quickly have been nothing short of astounding. More recently, we have started to witness technology’s influence on education. As Peter Haskell, math department chairman at Virginia Tech, said in a recent article, “How could [computers] not change higher education? They’ve changed everything else.”

Computers are indeed changing higher education, as well as elementary and secondary school education. The Danville School District in Indiana announced that it will be piloting an iPad-based program to educate its students by ability level and not by the traditional grade levels. Many see technology as the much-longed-for solution to the 21st century, individualized education that creativity expert, Sir Ken Robinson, espouses.

IMACS has been grouping students by ability level and using technology to provide customized learning experiences for over 20 years, and we’ve learned much in the process. We understand why it is tempting to leverage existing technology, as is, to try to improve education—development costs are little to none, and the solution seems to “fit” the problem “well enough.” However, our experience tells us that a more thoughtful approach yields better outcomes for the students involved.

The popular approach to incorporating technology in education seems to follow the “defense-to-daily life” path. By this we mean that amazing inventions first created for military purposes made their way into daily life after people asked, “How else can this be used?” Examples include digital photography, which came from spy satellites, and the GPS in your car that keeps you from getting lost.

Within the education debate, the analogous line of reasoning is, “We have the technology to distribute and exchange information on a global scale at relatively low cost. Education, in its most basic form, is information. Therefore, technology can be used to widely deliver education. Technology also enables us to track and analyze massive amounts of data. Student performance is essentially data. Therefore, we can use technology to determine when an individual student has learned a topic and is ready to study the next topic.”

One obvious problem is that this approach relies on quantifiable student performance, the kind that computers know how to “think” about. What’s that? None other than answers to multiple choice questions, stand-alone numeric answers, or simplistic word answers. In other words, this approach to individualized learning uses the type of assessment you find with one-size-fits-all standardized testing, which we know does not effectively measure mastery.

Consider the ability to apply learning to novel situations, which is a component of mastery that is generally recognized as the highest of the so-called “learning outcomes.” How could standardized test-like questions ever measure the ability to recognize underlying parallels and to transfer skills acquired in one context to another? Educational technology, while still a net positive, has its limits. It’s hard to imagine a situation in which a computer could reliably grade an essay on “Compare and contrast the lifestyles of the middle class in Manila, Philippines, and Quito, Ecuador.”

For technology to deliver on the promise of turning out well-educated students in greater numbers, methods should be developed for automatic evaluation of student performance that go beyond the multiple-choice paradigm. This includes designing questions that truly test the depth of a student’s understanding, along with systems to assess the quality of answers to such questions. In other words, the technology should be made to fit the curriculum and not the other way around.

Taking this approach means that one does not have to compromise on curriculum development. One has the freedom to create original course material based on what is shown to be effective, knowing that the technology to support it will follow. This is one of our founding principles at IMACS, where we have been researching, developing, and implementing these technologies in our online mathematics and computer science courses since the beginning. The depth of understanding that our students develop leaves us confident that we made the right choice for them.

Education reformers must decide if they will use the building momentum to spread mediocrity all over the place, or if they will push for the bold change necessary to teach students the 21st century skills that they need. Students deserve better than to have the technological tail wag the pedagogical dog.

For innovative courses in gifted math and online computer science, try IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

This week’s post by guest author, Dr. Dora Musielak, includes selected excerpts from her book, Sophie’s Diary: A Mathematical Novel. The story is inspired by French mathematician, Marie-Sophie Germain, the first and only woman in history to make a substantial contribution to the proof of Fermat’s Last Theorem. Little is known of Germain’s adolescence prior to the time she began corresponding with great mathematicians such as Lagrange, Legendre, and Gauss. As Dr. Musielak explains in the MAA Books blog post, this book imagines how Sophie might have learned mathematics on her own during a time when girls and young women were strongly discouraged from such pursuits.

An aerospace engineer scientist by training, Dr. Musielak is currently Researcher and Professor of Physics and Mathematics at the University of Texas Arlington. Dr. Musielak is also a NASA fellow. She is also the author of Kuxan Suum: Path to the Center of the Universe, a book to that combines astronomy and astronautics to promote the exploration of space.

From Sophie’s Diary: A Mathematical Novel

Wednesday — April 1, 1789

How can I divide 35 in a half, a third and a ninth, and get an even number? It seems impossible! Yet I know there must be a way… .

     My name is Sophie. Today is my thirteenth birthday and my parents surprised me with wonderful gifts. My father gave me a lap desk of glossy mahogany wood. It has a compartment to keep paper and pens, and a secret drawer that can only be opened by pressing a hidden tab underneath. When I unlocked it, I found a mathematical riddle and a note from Papa, challenging me to solve it. He gives me a year, but I hope to find the answer sooner than that. Oh, I am so excited!

     My mother gave me a porcelain inkwell, a stack of linen paper, sealing wax, a miniature burner, six bottles of ink in different colors, and a set of quills. These are the best birthday presents ever! I promised my parents to write often to improve my penmanship. Maman says writing neatly and correctly is very important for a refined young lady. This gave me the idea of writing a journal intime, a diary where I can record my innermost thoughts and feelings.

     I love my father. He taught me arithmetic when I was five. I still remember my excitement when Papa taught me the numbers. I used to think that the arithmetic operations were magic tricks to produce new numbers. Just for fun, I spent hours adding numbers to create others. Now I help Papa with the more complicated calculations he needs for his business transactions. He still calls me ma petite élève.

     I have two sisters, Angélique-Ambroise and Marie-Madeleine. Angélique is ten years old, a pretty and vivacious girl who talks incessantly, exactly the opposite of me. Madeleine is almost nineteen years old. She resembles our mother and, like her, she is romantic and sweet. I am not like either of them. My sisters like to dress in beautiful gowns, style their hair, and sing and dance. I don’t like any of that.

     Angélique calls me “peculiar.” She teases me all the time because I like to be alone and would rather read books. I do not care whether my hair is curled, or if my dresses are fashionable. I do not think about these things the way she does. But I am fond of her, just as I am of my mother and Madeleine. I especially love my father with all my heart; mon cher père, he understands me better than anyone.

Monday — January 2, 1792

I begin the new year with more determination and a renewed resolve to study prime numbers. One of my goals is to acquire the necessary mathematical background to prove theorems.

     Prime numbers are exquisite. They are whole pure numbers, and I can manipulate them in myriad ways, as pieces on the chessboard. Not all moves are correct but the right ones make you win. Take, for example, the process to uncover primes from whole numbers. Starting with the realization that any whole number n belongs to one of four different categories:

                   The number is an exact multiple of 4 : n = 4k
       The number is one more than a multiple of 4 : n = 4k + 1
       The number is two more than a multiple of 4 : n = 4k + 2
     The number is three more than a multiple of 4 : n = 4k + 3

It is easy to verify that the first and third categories yield only even numbers greater than 4. For example for any number such as k = 3, 5, 6, and 7, I write: n = 4(3) = 12, and n = 4(6) = 24; or n = 4(5) + 2 = 22, and n = 4(7) + 2 = 30. The resulting numbers clearly are not primes. Thus, I can categorically say that prime numbers cannot be written as n = 4k, or n = 4k + 2. That leaves the other two categories.

     So, a prime number greater than 2 can be written as either n = 4k + 1, or n = 4k + 3. For example, for k = 1 it yields n = 4(1) + 1 = 5, and n = 4(1) + 3 = 7, both are indeed primes. Does this apply for any k? Can I find primes by using this relation? Take another value such as k = 11, so n = 4(11) + 1 = 45, and n = 4(11) + 3 = 47. Are 45 and 47 prime numbers? Well, I know 47 is a prime number, but 45 is not because it is a whole number that can be written as the product of 9 and 5. So, the relation n = 4k + 1 will not produce prime numbers all the time.

     Over a hundred years ago Pierre de Fermat concluded that “odd numbers of the form n = 4k + 3 cannot be written as a sum of two perfect squares.” He asserted simply that n = 4k + 3 ≠ a² + b². For example, for k = 6, n = 4(6) + 3 = 27, and clearly 27 cannot be written as the sum of two perfect squares. I can verify this with any other value of k. But that would not be necessary.

Friday — May 31, 1793

… I discovered a bookshop specialized in mathematics, right on the corner of the quai des Augustins. The shop was empty when we entered, thus allowing me to browse without curious eyes and questioning stares. What I found is indescribable, a treasure of knowledge neatly recorded in the pages of those volumes. New books written by contemporary mathematicians and exquisite translations of ancient manuscripts, all bound in beautiful leather covers and inscribed with golden letters. I was glad that I brought a full purse and purchased Oeuvres d’Archim`ede for 30 francs. It is expensive but I couldn’t let go of it. The book begins with a biographical portrait of Archimedes, then it discussed his memoirs, and it is supplemented with a history of the arithmetic development in Greece.

     I don’t remember the walk back home, as I was anxious to return and read my treasure.

Note: If you enjoyed these select passages, please visit www.sophiesdiary.net to read more extensive excerpts.

Study university-level mathematics with online gifted math courses from IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

Unless you’ve been hiding under a rock for the past year, you’ll have noticed that the campaign to teach kids (and adults) how to code is everywhere you turn. As parents, politicians, and educators debate how to produce more graduates in technology fields, the push to introduce computing at an earlier age gets stronger. For example, MIT’s Lifelong Kindergarten group is collaborating on programming software aimed at kids in preschool to second grade. There are even board books for babies on HTML and CSS! We suspect that such novelties are more for tech parents’ enjoyment.

IMACS believes these efforts are well-intentioned and some, when implemented, will be well-designed. But before you click over to Amazon to buy your little drool monster a book on Web design, IMACS can offer you a few examples of how to introduce computational thinking to children through easy activities that are familiar to you, even if you think you’re computationally challenged.

Computational Thinking vs. Coding

This short and informative paper by Jeannette Wing, head of the Computer Science Department at Carnegie Mellon University, explains clearly what computational thinking is and is not. The following excerpted quote is a good summary of the focus of this blog post:

Learning to think abstractly is an essential skill if you want to succeed in computer science. It makes solving problems easier, which in turn makes working on those problems more fun. Notably, students can learn to think like a computer scientist without entering a single line of code into a computer. In fact, our experience in teaching CS is that writing computer programs is trivial for students who first develop computational thinking skills. Let’s see where in our daily lives we can show kids relatable examples to help them make the transition to abstract thinking.

Stacks and Queues

In computing, a stack is an object in which data expressions are stored and retrieved in such a way that the first data expression to be stored is always the last data expression to be retrieved. It is an example of a so-called Last-In-First-Out (LIFO) object. The same idea applies to various real-life constructs that young kids encounter, even babies who love board books.

Obviously, you can’t explain LIFO with words to a baby and expect the baby to understand, but you can certainly demonstrate the concept with your actions. Take the classic Fisher-Price Rock-a-Stack, for example. Start with the rings off the cone and then load them on in the intended manner with the blue ring going on first. Try to get just the blue ring off. Can you do it while the other rings are still on the cone? No, you have to take the rings off one by one with the blue ring coming off last.

Older kids can appreciate the same concept with examples they come across in their lives: unloading plates from the dishwasher into the cupboard, setting the table with said plates the next day, selecting a product such as cosmetics from a store shelf, putting said product back if you decide not to buy it. You get the picture.

A queue is similar to a stack in that it is an object used to store data expressions. In the case of a queue, however, the first data expression to be stored is always the first to be retrieved. Queues are examples of First-In-First-Out (FIFO) objects. Kids encounter them every time they go through a checkout line or a drive-thru. Switch that Rock-a-Stack cone for an empty paper towel roll, and you’ve got yourself a baby-friendly queue.

Sorting Algorithms

Sorting is one of the oldest problems in computer science. Although the end goal (an ordered list) is conceptually easy to understand, getting there can be complex. Add to that the need for sorting algorithms to be computationally efficient and you’ve got yourself an interesting abstract puzzle.

If your kids are old enough to know or learn how to put words in alphabetical order, then make a project out of sorting the books on their bookshelf. Decide on a sorting key such as title or author’s name. For this example, we’ll use title. For the first shelf, ask your child to try a simple bubble sort. Traverse the shelf from left to right, compare the titles of two books, and swap them if they are in the wrong order. Repeat this process until all books on this shelf are in the correct order.

For the next shelf, you can use a simple insertion sort. Take all the books off that shelf and put them in order one by one in a pile on the floor. Each time that you add a book to the ordered pile, be sure to put it in the right place relative to the books that were previously added.

Now that you have two properly sorted sets of books, you and your child can work together to sort all books. Sounds like a good time to use a merge sort. Move the sorted books off the first shelf into another pile on the floor while keeping them properly ordered and separate from the pile of books from the second shelf. Reshelve the books as follows: repeatedly compare the titles of the two books that are atop the two piles, selecting the one that goes first, and continuing until both piles are exhausted.

Object Oriented Programming

An “object” in computer programming is a complex structure containing data fields and instructions. These objects interact with each other to create even more complex computer programs. The beauty of object oriented programming is that you can reuse objects to do common computing tasks without having to reinvent them each time. Over time, programmers can build up a “library” of useful objects.

The following analogy certainly isn’t perfect, but it will help get the point across about these seemingly mysterious objects. If you’re planning an outing with kids, you’ll need a few things to help keep your sanity: nourishment, entertainment, and possibly a change of clothes. So grab three bags and make some objects! In the nourishment object, you’ll probably need fruits, carb snacks, a protein, and beverages. For the entertainment object, how about art supplies, books, sporting equipment, and portable gaming device? Kids are made to get dirty, and the weather may change, so pack a top, bottom, and outerwear in the clothing object. Throw those “objects” in your huge tote “library” and you’re ready to go!

Think Like a Computer Scientist

Planting the seeds of computational thinking, especially the ability to think abstractly, is really a matter of recognizing the examples in your life that can be used to foster discussion with your children. Like any new endeavor, remembering to look at events in a computational light takes practice. You might just find yourself thinking like a computer scientist when it comes to solving the data problems in your own adult life.

Enhance your computational thinking skills with online computer science courses from IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

In our prior blog post where we discussed the importance of effective teachers for gifted students, we also made the point that such teachers should be armed with higher quality curricula better geared toward bright kids. This week, we delve more deeply into what raises the quality of curricula and renders them more suitable for bringing out the best in talented students.

Fast Forward vs. Delve Deeper

Let’s start with the obvious. Gifted students often understand new information after having it explained to them once. This is in contrast to a typical student who benefits meaningfully from review and reinforcement of new topics. There may be times when gifted children benefit from review, but they generally find repetition unutterably boring. Consequently, bright kids who are subjected to curricula that emphasize review can develop a dislike for school or, in the worst case, of learning.

Advocates of free online resources often point to online technology as a remedy in situations like this because you can skip over the boring parts of a lesson and cover more topics. But who wants to spend time and mental energy searching through a lesson to avoid the repetitive parts? More importantly for talented children, are we really aiming for quantity of topics over quality of learning as a badge of honor for the brightest among us? Gifted students’ time would be better spent gaining a deeper understanding of a subject using material that was specifically designed with their ability level and thirst for knowledge in mind.

Challenge and Failure as Preparation for Success

Online curriculum development for talented students is about more than just going faster and avoiding repetition. It’s about presenting challenging ideas along with the appropriate interactive tools to explore and understand them. It’s about asking questions that require genuine thought to answer rather than just a cursory understanding—or worse, a simple memory—of something. It’s about asking questions in such a way that, in the process of determining the answer, the student’s understanding gets deeper.

Parents and administrators should recognize that accelerating through standard curricula is not the same as studying coursework designed to challenge the gifted mind. Challenging talented students is essential for putting them on a path toward future success. These kids have the potential to solve our most intractable problems and invent products and processes not yet imagined. As anyone who has accomplished even one of these amazing feats will tell you—it’s not a sprint but a marathon fraught with many false turns. This relates to the much-quoted findings by Stanford psychologist Carol Dweck that praising intelligence undermines motivation and performance as compared with praising effort. A child who has not learned to put forth great effort in conquering ability-appropriate challenges or in developing resilience in the aftermath of failure will never reach his or her full potential.

Address Misunderstandings Immediately

For many subjects, including mathematics and computer science, ideas learned at one stage serve as the foundation for learning more complex ideas at later stages. Likewise, a misunderstanding of an earlier concept jeopardizes the understanding of future concepts that build upon it. It can be difficult to dislodge misconceptions that have had some time to settle:

Thus, any praiseworthy online education program should cause students to address a misunderstanding at the moment that they are having it. If you wait until some later time to give a student corrective feedback on their work, the moment of maximum learning has already passed. Remember that we’re talking about young students who are simultaneously learning various new ideas across multiple subjects. When a student is already focused on learning the next topic, it’s less effective to try to bring his or her mind back to an “old” idea.

How an online education program goes about detecting and addressing flaws in student understanding is critical to whether the program is really delivering on its promise to teach in the truest sense of the word. This is not a trivial exercise that can be accomplished by a system that instantly tells you whether a multiple choice selection or one-word answer is correct. Gifted kids can typically regurgitate information from memory or reflect back basic knowledge without much effort. But this doesn’t mean that they understand a topic at a depth commensurate with their ability. Any online curriculum that purports to educate yet relies on several, even many, simply structured questions as a measure of true understanding is short-changing its students, especially the bright ones.

Simply put, talented online students deserve curricula that address their unique intellectual needs along with technological tools designed to fit the particular curriculum and not the other way around. They deserve more than the same material they can get in school with improved presentation and a fast-forward button. Delivering on the promise of educating students online is possible, but it takes much more thought, planning, and investment to do than is widely accepted in the current media coverage and commentary.

Are you a gifted and talented middle or high school student? IMACS offers online courses designed just for you! Take our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

Mathalicious blog recently posted a well-written and compelling article about the consequences of our nation’s sudden elevation of the popular video tutoring Web site, Khan Academy. If you haven’t read the piece, you absolutely should because it explains beautifully the key reasons why parents and school administrators should be cautious about jumping on the bandwagon of free, technology-based resources as a means of effective teaching.

We won’t rehash here what’s already been said well by Mathalicious, nor do readers of this blog who like KA need to rally to its defense. IMACS acknowledges that KA is a valuable resource that has a place in the overall education portfolio for many students. But we also strongly believe that KA, or whatever the next free resource to be Web-ified is, is no substitute for high-quality curricula and the effective teaching thereof. This is particularly true for gifted and talented children.

Free Resources Are Good at Presenting Information and Sparking Curiosity

Children, bright ones in particular, are born self-directed and self-taught. As they enter school and progress through the regimented structure of age-based, test-driven instruction, it’s no surprise that this natural thirst for learning diminishes. For a gifted child this is intellectual torture, and the pain has only spread across our nation as budget cuts erode the quality of or eliminate altogether public school gifted programs. So it’s no wonder that many talented children and their parents have come to value a Web site like KA.

What’s not to like? KA offers a myriad of topics for a curious mind to explore. You pick which video to watch, and you decide when to move on if it’s boring. And KA’s founder, by most accounts, is pretty good at explaining concepts in a non-threatening way. For typical kids, this can be a superior alternative to classroom instruction. For gifted kids, this is a wonderful way to spark curiosity and access above-grade-level material. Those of us from an older generation are reminded of cherished times flipping through encyclopedia volumes, letting the books fall open where they may, and reading about some new topic that we’d never heard of before. Whereas the World Book cost parents a small fortune and took up a big chunk of bookshelf space, KA is free and fits on the smartphone in your pocket! So far, so good. Here comes the “but.”

Pedagogy Still Matters, Especially for Mathematically Talented Kids

But how does that spark become a burning fire of passion, dedication, effort, and tenacity—qualities necessary for a gifted child to achieve his or her full potential? A key component of the answer is teachers. More specifically, teachers who understand how to inspire bright children, who can guide them when they struggle, and who know how to unleash the power of their natural talent. Optimally, these teachers should be armed with higher quality curricula better geared toward kids who only need to be told things once. They should have the experience to know that the places where talented kids struggle are often different from the usual stumbling blocks for the general population, and they should understand that high-fliers sometimes need help in overcoming the fear of failure.

Nowhere is this more evident than in math where the abstract nature of its concepts and language call for an experienced and interactive guide. To a gifted child, the difference between one-way, rules-based, memorization-laden math instruction and student-involved, teacher-guided, reasoning-based interaction is like intellectual starvation versus a bountiful feast. The nourishing environment of the latter allows mathematically talented minds to devour, understand, apply, and sometimes grow the body of knowledge. No pre-recorded video that restates, however pleasantly, the usual instruction found in US math classes, with the added benefit that you can rewind and repeat for reinforcement, is going to elevate a mathematically bright child to the next level.

Bright Online Students Should Have Access to Supportive Instructors

At IMACS, we made a deliberate choice to use an interactive teaching approach that incorporates substantial student-led exploration guided by effective teachers. Our collective experience on how talented kids learn best, which questions they tend to ask, and where and why they tend to struggle has been gathered over decades of teaching our curriculum in a classroom setting. This wisdom has been painstakingly built in to our eIMACS online courses, which feature tools that provide immediate feedback at exactly the moments students most frequently need it.

Needless to say, a gifted child is wonderfully unique and creative. So it comes as no surprise to us that our students come up with questions from time to time that we hadn’t anticipated. This is exactly why each eIMACS student is assigned a principal IMACS instructor to answer these questions and provide individualized guidance when needed.

We know what you’re probably thinking, and yes, this blog post is self-serving. But it’s also what we genuinely believe because we’ve borne witness to the success of these ideas, having taught thousands of bright students this way over the years. As such, we feel compelled to share our experience with readers, especially parents and others who may be making decisions now or in the future on how to best foster mathematical talent (or any talent for that matter). As with coaching in elite athletics, effective pedagogy is essential to the full and fulfilling intellectual development of gifted children, and its value should not be discounted so readily. Don’t let talk of free videos convince you otherwise.

Looking for online courses in gifted math and computer science with top-notch teachers? Try IMACS! Take our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

Did you know that eIMACS serves students in over 10 countries around the world? This week, our blog post features current student, Hossain Md. Jihad Turjo. Turjo is a talented 11th grader at Mastermind School in Dhaka, Bangladesh. In addition to excelling in his eIMACS courses, he has also earned top marks from other prestigious online programs for bright students, including Johns Hopkins Center for Talented Youth (CTY) and Stanford’s Education Program for Gifted Youth (EPGY). When not immersed in his studies, Turjo enjoys reading novels and has even had three published book reviews for CTY’s Imagine magazine:

• “Guns, Germs, and Steel: The Fates of Human Societies” by Jared Diamond
• “H.I.V.E.: Higher Institute of Villainous Education” by Mark Walden (Click on the ‘Preview’ button to read Turjo’s review.)
• “The Boy Who Harnessed The Wind” by William Kamkwamba and Bryan Mealer

How did you first become interested in computer science?

My first programming experience of any sort was at school in 8th grade – we had the basics of Visual Basic as part of our coursework curriculum. There were quite a few incidents which hooked me to programming during the six months or so that I had Information and Communication Technology (ICT) at school as part of my curriculum. An example of such a case would be when we were learning to program a calculator for adding numbers with the digits 0, 1 and 2. The “calculator” would have virtual “buttons” labeled +, 0, 1, 2 and =, and would have a screen for displaying the numbers typed in or the result.

Of course, the very thought was horrid to me – the numbers lacked 70% of the digits, and I could only do addition. At the moment, our teacher was not inclined to be very explorative either. So I decided I could do better, and pretty soon I had a calculator with all the digits, an operation display alongside a numbers display, all the operations instead of simply addition, and functions for taking nth roots, raising numbers to any exponent and reciprocating numbers.

That was the kind of small trivial thing that later snowballed into a massive interest in computer science and programming – and eIMACS was perfect for it.

Residing in Bangladesh, how did you find eIMACS, and what made you decide to take one of our online computer courses?

I found eIMACS while browsing the net for computer science courses that are on offer for young and talented students. So I made an inquiry about what courses might be on offer for me, considering that I was a complete amateur in the field of computer science. The next day, I spoke on the phone with a senior IMACS instructor who suggested that I start off with University Computer Science I, that apparently being a very good beginner’s course. So I took the Aptitude Test, managed a good enough score, and started the course that very day. I guess the main deciding factors in what made me choose eIMACS was the promptness and enthusiasm of the instructor’s reply, the fact that he offered to be my instructor even though I was a novice, and the course description on the IMACS Web site.

As a student who has taken or is taking several online courses in math and science from different vendors, how did your experience with eIMACS compare?

In addition to UCS1 from eIMACS, I have taken Honors Chemistry, Honors Biology, and AP Calculus BC from CTY and AP Physics C: Mechanics from EPGY. I am now continuing AP Statistics from Northwestern University’s Center for Talent Development (CTD).

The courses from eIMACS and CTY were all self-paced allowing me to work on the lessons and the tests at whatever time suited me most, contrasted against a fixed course in which lessons are taken by an instructor, normally during his office hours. That was a thing I really liked about eIMACS and CTY – the self-paced option, seeing that a fixed course would be extremely hard for me to keep up with due to the huge time zone gap. Also the quality of presentations for both the eIMACS and CTY courses was really high.

CTD’s AP Statistics course, which has been a satisfactory experience thus far, is next best, and then EPGY’s Mechanics course after that.

UCS1 from eIMACS is the clear winner when it comes to the best course among these. It started at a very basic level in a way that made it extremely easy for me, a novice to understand. I loved the user interface and the way computer science code was introduced to the rookie. The course got progressively more challenging and, I might add, more fun. An awesome thing about UCS1 was the way the tests were taken entirely online. I mean, it is kind of tedious to have to write out answers on a give question paper, scan it and then e-mail it, the way I did it with CTY. But given that one was a math course, where steps and working are extremely important, I guess that was the most suitable option for CTY.

As to instructor availability, I think it’s reasonable enough to say my IMACS instructor was the one I had the most contact with. He was simply more cheery, more communicative and more encouraging than my instructors from the other programs. I’m not saying the others didn’t have those qualities, but my IMACS instructor had it to a great extent.

UCS1 is taught using the programming language Scheme, whereas many introductory courses take students straight into Java, especially since the College Board’s Advanced Placement exam is currently in Java.  What’s your view on the eIMACS approach?

I felt that UCS1 did an awesome job in introducing me to the field of computer science. The approach of using Scheme seems to me to be much better. I have seen Java code for web pages a few times, and it did look quite a degree more complex than Scheme. Hence I would say the IMACS approach in using a simpler language (simple is a relative term) as a beginning language is all the more effective for its simplicity. I found I was able to focus on learning the programming concepts instead of worrying about whether I was getting the syntax right. And if anyone was very interested in Java, they can always take the AP Computer Science course from IMACS. So I would say that the IMACS approach is a very effective method.

Your goal is to major in computer science at a US university. What would you like to do after that? Do you have a career vision in mind?

I would simply love to become a top programmer or “Head Game Designer” at someplace like Microsoft or Sega. There are some pretty awesome games out there and someday I want to be the one bringing to life better themes than those games did, coupled with a much better game-playing experience. Sky Target and The House of The Dead series are classics that are impossible to forget – both Sega productions. Someday I hope I can do better.

IMACS delivers flexible and high-quality online computer science courses anywhere in the world. Register for our free aptitude test. Play along with our weekly IMACS logic puzzles on Facebook.

Note: This story is adapted from our IMACS Math Enrichment Program for talented students in grades 1-8. The solution and analytical process are revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!

Max, The Lost Dog
Sofia, a bright IMACS student, has lost her dog, Max. Luckily, Max was wearing a collar when he was found by another IMACS student, Emily, who loves using her logical reasoning skills to solve mysteries. Tucked into the collar was a piece of paper with clues on where to return Max should he become lost. Follow the clues to help Emily find which house is Max’s so that Sofia can be reunited with her dog … and possibly make a new friend in Emily. (Since both girls take online math classes through eIMACS, they had not met each other yet.)

Clue 1: The number of the house where Max lives is the sum of two numbers, each of which is a power of 2 that is greater than 0 and less than 10. These two numbers that add up to equal Max’s house number can be the same, but they don’t have to be.

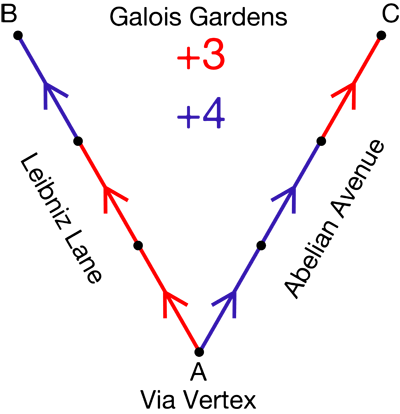
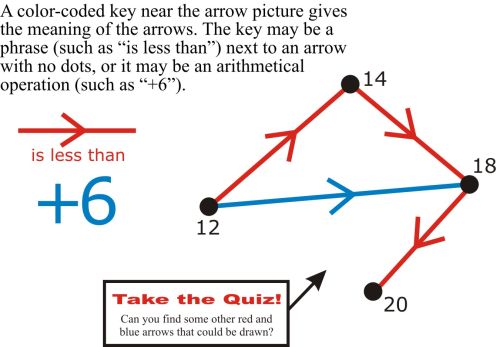
Clue 2: Max lives in Galois Gardens, a neighborhood represented by the following arrow diagram in which each dot represents a house.

The fork to the left is Leibniz Lane, the fork to the right is Abelian Avenue, and the house at the bottom is on Via Vertex. Here is how you interpret the arrows:

• The house number at the end of a red arrow is equal to the house number at the start of that red arrow plus 3.
• The house number at the end of a blue arrow is equal to the house number at the start of that blue arrow plus 4.

Clue 3: The biggest number for any house in the neighborhood is 15.

Clue 4: The number of the house where Max lives is a multiple of 3.

The Analytical Process of Solving the Mystery
Now that you’ve given yourself a chance to work through the problem, let’s go step by step to understand one way we can think about putting the clues together.

Clue 1: What are the powers of 2 that are greater than 0 and less that 10? They are 1=2⁰, 2=2¹, 4=2², and 8=2³. So we need to take one number from the set {1,2,4,8} and a second number from the same set {1,2,4,8} and add them together to come up with the list of possible house numbers. Remember that both numbers can be the same but do not have to be. We’ll leave the arithmetic to you, but we should all arrive at the following possibilities:

Clue 2: Although we don’t yet know any of the house numbers in the arrow diagram of the neighborhood, what can we figure out from the information given? One thing is the location of the house with the smallest number. It has to be the house at the bottom of the picture because the arrows tell us that every time you go from that house along either of the two roads, you add 3 or 4 each time. So you keep getting bigger and bigger house numbers, and they never fall back below the number you started with at the bottom, whatever that number is.

Likewise, is there anything we can say about the largest house number in the neighborhood? Well, it’s probably at the top of the diagram since the house numbers get bigger as you go up the roads. But is it the house on the top left or the one on the top right? Now we need some variables now to help us keep track of these houses.

Let’s call the house number at the bottom “A,” the one on the top left “B,” and the one on the top right “C.”

We know B is bigger than A, and C is bigger than A. Can we say anything about how much bigger B and C are than A? Well, to get from A to B, we add 3 and 3 and 4. That is, we add 10 = 3 + 3 + 4. So A + 10 = B. To get from A to C, we add 4 and 4 and 3. That is, we add 11 = 4 + 4 + 3. So A + 11 = C. We’re starting with at same number, A, and adding 11 to get to C but only 10 to get to B, so C must be bigger than B. Now we know that the house with the biggest number is on the top right.

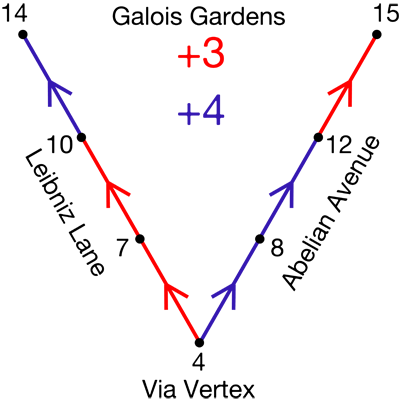
Clue 3: This clue, along with what we figured out from Clue 2, tells us that C = 15. In other words, the address of the house at the top right is 15 Abelian Avenue. With a little arithmetic, we can now determine the rest of the addresses in the neighborhood as follows:

Now that we have all the addresses in the neighborhood, we can go back to our original list of possible house numbers from Clue 1 and cross off the ones that do not show up in the neighborhood. Here’s what our list should look like now:

Clue 4: We’re down to only three possible house numbers—4, 8, and 12. Clue 4 tells us that the house number is a multiple of 3. Which of these possibilities is a multiple of 3? Only 12 is a multiple of 3. Hooray! We figured out where Max lives—12 Abelian Avenue! Sofia will be so happy to have Max back at home, and Emily will be quite pleased with herself for having solved the mystery and done a good deed.

Show a child some tricks and he will survive this week’s math lesson. Teach a child to think critically and his mind will thrive for a lifetime.

Math word problems confound many students for a variety of reasons. Too often, well meaning parents and teachers attempt to help students struggling with these kinds of problems by offering them tricks or shortcuts for getting to the solution without necessarily understanding what’s going on. Just do an internet search for something like “how to solve word problems,” and you will get a slew of Web pages with tips, tricks and strategies like the following:

• Search for key words that will tell you which mathematical operation you should use (e.g., “lost” means subtraction).
• Cross out non-essential information so that you are not distracted by it.
• Draw a picture to illustrate each step of a problem.

Let’s consider these three examples for a moment. To suggest that looking for key words within the text of a math problem is somehow a “strategy” to solving it more easily seems a bit absurd. Basic reading comprehension skills are obviously essential to solving any problem, math or otherwise, where the information is communicated via natural language. No key word mapping is going to provide a fool-proof way of understanding what a word problem is asking. If you’re starting with a word problem that is well designed and written with clarity, there simply is no “trick” to understanding the words.

The other two examples sound reasonable on the surface, but a closer examination reveals problems with them too. To determine which pieces of information are relevant to the solution (as in Example #2), you need to be able to evaluate and analyze the given information. To correctly translate the words of a problem into a step-by-step illustration (as in Example #3), you need to be able to understand and prioritize the information. In other words, tricks like these seem to require the very skills needed to solve the problem without the tricks! Furthermore, a “tip” cannot tell you whether you have enough information to solve the problem, or how to find any missing information. Only critical thinking and logical reasoning skills can help you there.

This approach of relying on “clever strategies” to replace critical thinking runs counter to the IMACS philosophy of teaching children the fundamental skills they need to solve problems throughout their lives, whether they be elementary word problems or complex Calculus problems, whether it’s making correct change or correcting the flight path of an exoplanet-bound space craft.

Meaningful Strategies That Matter
While silly tricks may work for some students as a short-term fix to “just get through the problem,” there are practical and helpful techniques that should be part of any meaningful approach to understanding and solving word problems.

Pay attention to units of measurement. Word problems commonly feature units of measurement. When finding a solution, it’s important to pay close attention to how you are adding, subtracting, multiplying, or dividing amounts in the problem so that you don’t end up combining “apples and oranges.” If you carefully track the units of measurement through each step of your computation, you can compare the units of your answer to what it should be based on the question. This is a good technique to check the reasonableness of your answer rather than one that “magically” solves the problem for you. Here’s an example:

No one would think that the following approach is right

because adding children to cookies makes no sense! The answer requires a relationship in the form of “X cookies per child” – or, more algebraically,

With this in mind, what makes sense is the following:

While we’re on the topic of cookies, here’s another example:

Most people know to do something with ( 4,500 / 3 ) and 5, but what? Looking at the question in the problem, we know that our answer should be in the form of “X cookies.”

What if we set up the equation correctly

but then worked out our answer as follows?

Hmm … 300 cookies per minute per minute? The fact that our answer is not measured purely in cookies as expected tells us that we made a mistake in our calculation.

Use reverse word problems to practice abstract thinking. The process of solving word problems often requires us to connect a real-life situation described in language we know with the abstract version written with variables and equations. As with learning to speak a foreign language, thinking abstractly becomes more natural with practice and regular use, and the earlier you start, the easier it is.

When kids are younger, parents can help them to develop an intuition for abstract reasoning by doing “reverse” word problems in the guise of creative play. Start by writing down an equation such as 7 + ___ = 10. Next, ask your child to imagine a story that goes with this equation. He might say something like, “It takes 10 gold stars to get extra recess, and I already have 7. How many more stars do I need?” For 3 + (8 × 2) = 19, she might say, “When I started robotics, I took 3 introductory classes. Then, I took 2 classes per week for 8 weeks. So, I have taken a total of 19 classes.”

Be sure to keep the level of difficulty appropriate for your child’s math ability. Frustrating him with a computationally hard problem will only defeat the purpose of teaching him to think abstractly.

Word problems can be used effectively to teach important mathematical concepts and to help give real-world context and purpose to what may seem like useless hieroglyphics to some people. But without a firm foundation in critical thinking and logical reasoning skills, a student is sure to be at a disadvantage when trying to evaluate, analyze, prioritize, and synthesize the numerous pieces of information embedded in the narrative. Tips, tricks, and strategies may help at the margins, but there is simply no substitute for genuine understanding.

Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.

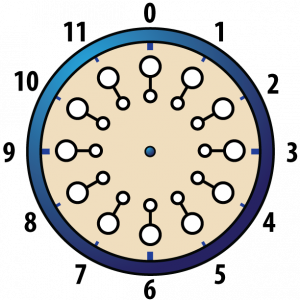
In our previous IMACS blog post on modular arithmetic, we introduced the Clock Game as a fun way to teach children about modular addition. Now, we’ll introduce a few variations on the Clock Game that make it more interesting. If you’re not familiar with the Clock Game, we suggest that you first read our introduction to modular addition before adding on with this post. Have fun!

The Double Game

In the double game, there are two pieces at each number at which to play instead of just one.

The game described in our introduction to modular addition can also be played as a “double game.” The only difference is that when playing double games, a player has more choices. For example, if, as a result of a particular move, a player has to place a checker at a number, one of whose circles is unoccupied and one of whose circles is occupied by the opponent, the player has the choice of either taking the opponent’s checker by replacing it with one of his or her own, or placing a checker on the unoccupied circle and leaving the opponent’s checker on the math. Double games, therefore, last longer, since all the available places must be occupied before the game is over.

Kings and Double Kings

Another variation of the games which can make them more interesting involves the use of kings and double kings. Only one place at each number is used in these games. In this variation, if the move requires it, you may place a second checker on top of one of yours already occupying a particular position, thus creating a “king checker.” If you have a king checker already occupying a certain position, then, if the move requires it, you may place a third checker on top of the king, thus making a “double king.” If a double king occupies a particular position, no further checkers may be added to the pile and so the play continues as in the simplest version of the game.

If your opponent would normally land on a place where you have a double king, then that double king cannot be removed, and the opponent cannot place a second checker. The hour hand, however, should still be moved so as to point at the position occupied by the double king even though your opponent could not place a checker there. If, however, your opponent lands on a place where you have a king, then both your checkers may be removed and replaced by one of your opponent’s checkers. The game ends when all of the positions are occupied by at least one checker upon the completion of a turn. This type of game is scored by counting 3 points for each double king, 2 points for each king, and 1 point for each single checker.

Kings, Double Kings and the Double Game

This variation utilizes the rules of the last two sections simultaneously. The first checker of each move must be placed on an unoccupied position, but there may be several choices for the second checker. For example, suppose your second checker has to be placed at “3,” your opponent has a king on one of the positions labeled “3,” and you have a checker (or a king) on the other position labeled “3.” You may either remove your opponent’s king and replace it with one of your own checkers, or you may form a king (or a double king) of your own. In such a situation, you may always choose either one of the two possibilities offered you by the two positions corresponding to the number at which your second checker is to be placed.

IMACS pays tribute to Belgian mathematician and mathematics educator, Georges Papy, who died in Brussels this past November at the age of 91. Georges and his wife, Frédérique, also a noted mathematics educator, were two of the seminal figures in the development of what eventually became the IMACS Mathematics Enrichment curriculum. We are deeply grateful to the Papys for their life’s work on behalf of mathematics students and their teachers.

The Early Years

Georges Papy was born in Anderlecht, a municipality in Brussels, Belgium of not quite seven square miles, on November 4, 1920. World War I had ended just two years before, and the country, which had suffered immensely under four years of German occupation, was still recovering. Against this backdrop and coming of age during the rise of Hitler, it is no wonder that young Georges was a member of the armed underground resistance forces in Belgium during 1941 – 45, serving in particular in the areas of intelligence and action. An educator from the start, he taught clandestine courses to students at the University of Brussels during 1941 – 42, and taught in a clandestine school for Jews during 1942 – 43 in the town of Méan, 50 miles to the southeast of Brussels.

After the end of World War II, Papy earned his doctorate in mathematics (with the highest distinction) from the University of Brussels in 1945, and was granted his advanced teaching diploma by the Science Faculty of the University of Brussels in 1951. After serving from 1949 first as Reader and then as Senior Lecturer at the University of Brussels, he became Professor of Algebra in the Science Faculty in 1956. The year before, he became a member of the prestigious Institute for Advanced Study in Princeton, New Jersey.

Finding His Purpose: Mathematics Education

During the mid 1950s, influential academic mathematicians were leading efforts to improve the quality of mathematics education in France. In parallel with these developments, Georges became deeply interested in improving the quality of mathematics education at the secondary school level, and assumed a position of leadership in Belgium of what became known as the New Math movement. [This was inspired in part by a colloquium organized in 1959 in Royaumont, France, by the agency that in 1963 would become the OECD. A follow-up meeting held in Yugoslavia under the chairmanship of the American mathematician Marshall Stone gave rise to a secondary school mathematics curriculum that was published in Paris in 1961 under the name “Mathématiques nouvelles” (“New Math”).]

Papy’s work in mathematics education would accelerate quickly from that point. In 1961, he founded the Centre Belge de Pédagogie de la Mathématique (Belgian Center for Mathematics Pedagogy). From 1962 onward, Georges was called upon as an expert in mathematics education by several international groups, including UNESCO, IBM, and the OECD. During 1960 – 70, he served as president of the Commission Internationale pour l’Étude et l’Amélioration de l’Enseignement des Mathématiques (International Commission for the Study and Improvement of Mathematics Teaching), and was founding president of the Groupe International de Recherche en Pédagogie de la Mathématique (International Research Group in Mathematics Pedagogy), starting in 1970. Amid this flurry of activity, Papy even found time to serve as Senator in the Belgian government during 1963 – 64.

Modern Mathematics: A Crowning Achievement

During 1963 – 66, with the collaboration of his wife, Frédérique, Georges published the groundbreaking six-volume series entitled Mathématique Moderne (Modern Mathematics), which represented a fundamental reformation of the secondary school mathematics curriculum based upon the unifying themes of sets, relations, functions, and algebraic structures (such as groups).

His mathematical educational interests expanded to include elementary school education. Starting in 1967, under the auspices of the CPBM, Frédérique and an associate taught experimental mathematics classes to six-year-olds. In the years that followed, Papy and Frédérique published several volumes comprising what amount to annotated accounts of these experimental classes and those that succeeded them. The mathematical underpinnings of this elementary school work remained the same as those of Papy’s earlier secondary school work, prominently featuring the use of multicolor arrow diagrams to represent relations and functions.

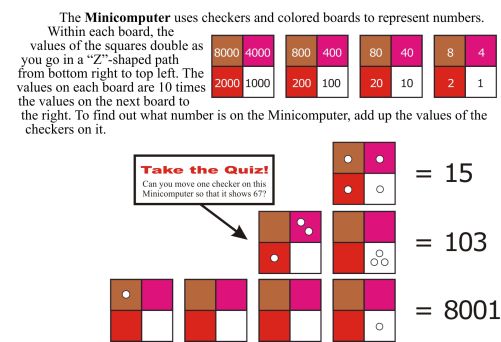
The Papy Minicomputer

As part of this work at the elementary school level, Papy developed what became known as the Papy Minicomputer and published a related text, Minicomputer, in 1968. This is a two-dimensional, mixed binary/decimal abacus made of square boards subdivided into four squares, each color-coded with Cuisenaire rod colors. He attributed the design of the Minicomputer to some work by the renowned Belgian cosmologist Msgr. Georges Lemaître (who was the first to propose what he called “The Primeval Atom” but which Fred Hoyle disparagingly labeled “The Big Bang Theory”). In the mid-1950s, Lemaître had proposed the introduction of new digits to represent numbers. The digits were formed from lines and curves that revealed an underlying binary structure. Papy adapted this idea and transformed it into a two-dimensional board on which checkers may be placed.

The IMACS Connection

In 1969, Georges and Frédérique met IMACS founder Burt Kaufman at the first conference run by the International Commission on Mathematics Education in Lyon, France. At the time, Burt was the director of a federally-funded mathematics curriculum research and development project called the Comprehensive School Mathematics Program. He managed to recruit Frédérique as his Director of Research, a role that she fulfilled during 1973 – 78. Of course, this meant that Georges paid frequent visits to the United States. Consequently, he and his wife had a very significant influence in setting the direction for the development of what has now become the IMACS Mathematics Enrichment curriculum.