Note: This story is adapted from the IMACS “Elements of Mathematics” series of textbooks and is based on modular arithmetic. This topic is typically covered in the first year of EM, which is often taught to talented 6th graders. The solution is revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!
The Stolen Jewel of Rainsmore
In the town of Rainsmore someone has stolen a precious jewel. A very famous detective, Roy Henshaw, has been called in to solve the crime. After a great deal of questioning, Detective Henshaw has narrowed the number of suspects to a small group.
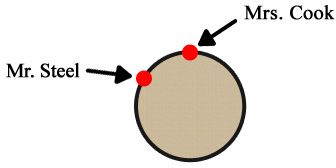
Late Wednesday night Henshaw seats the suspects around a table and begins questioning with Mr. Steel. Then he questions Mrs. Cook.
After Mrs. Cook has been questioned, Henshaw continues around the table in order, being very careful to skip no one and to ask each person a different question.
The questioning continues through the night with Henshaw getting closer to finding the thief.
By 5:00 in the morning Henshaw has asked hundreds of questions and, being such a famous detective, he has kept track of which questions each suspect has answered:
Mr. Steel has answered questions 1, 8, and 15.
Mr. Gunn has answered questions 3, 10, and 17.
Mr. Decker has answered questions 12, 19, and 26.
Mr. Jones has answered questions 11, 18, and 25.
Mrs. Cook has answered questions 2, 9, and 16.
Henshaw now has some important questions for which he needs answers. You should answer them if you are to solve the mystery.
a) How many people were seated around the table?
b) Who answered the 4th question?
c) Who answered the 5th question?
d) Who answered the 24th question?
e) Who answered the 31st question?
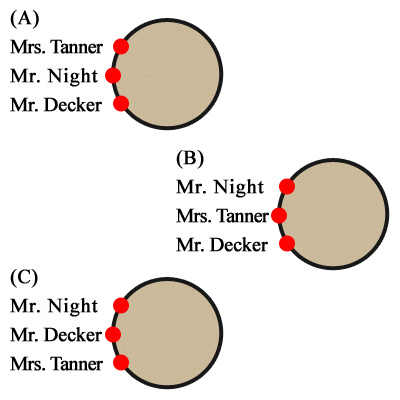
f) Detective Henshaw also noted that Mrs. Tanner answered question 70 and that Mr. Night answered question 48. Which of the following pictures shows the correct seating around the table of Mr. Night, Mrs. Tanner, and Mr. Decker?
g) Aha! Henshaw now knows who the thief is. His extremely clever and searching mind has unmasked the criminal.
THE CRIMINAL IS NONE OTHER THAN THE PERSON WHO ANSWERED THE 37TH QUESTION.
Who is the thief?
Has traditional school stolen your passion for learning? Find it again with engaging courses in gifted math and computer science online from IMACS! Register for our free aptitude test. Play along with our weekly IMACS logic puzzles on Facebook.
Answers:
a) Seven
b) Mr. Jones
c) Mr. Decker
d) Mr. Gunn
e) Mr. Gunn
f) Table (A)
g) Mrs. Cook
Note: This story is adapted from our IMACS Math Enrichment Program for talented students in grades 1-8. The solution and analytical process are revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!
Max, The Lost Dog
Sofia, a bright IMACS student, has lost her dog, Max. Luckily, Max was wearing a collar when he was found by another IMACS student, Emily, who loves using her logical reasoning skills to solve mysteries. Tucked into the collar was a piece of paper with clues on where to return Max should he become lost. Follow the clues to help Emily find which house is Max’s so that Sofia can be reunited with her dog … and possibly make a new friend in Emily. (Since both girls take online math classes through eIMACS, they had not met each other yet.)
Clue 1: The number of the house where Max lives is the sum of two numbers, each of which is a power of 2 that is greater than 0 and less than 10. These two numbers that add up to equal Max’s house number can be the same, but they don’t have to be.
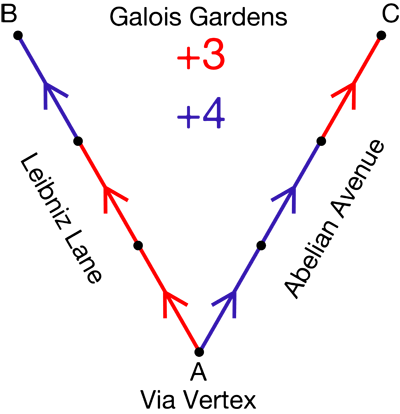
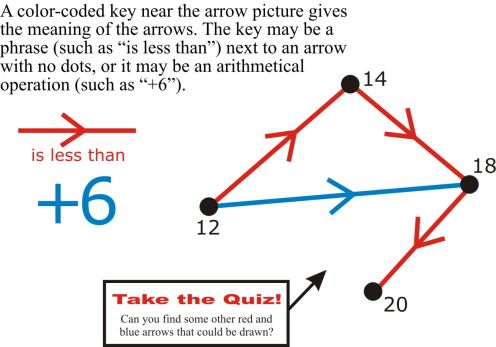
Clue 2: Max lives in Galois Gardens, a neighborhood represented by the following arrow diagram in which each dot represents a house.
The fork to the left is Leibniz Lane, the fork to the right is Abelian Avenue, and the house at the bottom is on Via Vertex. Here is how you interpret the arrows:
• The house number at the end of a red arrow is equal to the house number at the start of that red arrow plus 3.
• The house number at the end of a blue arrow is equal to the house number at the start of that blue arrow plus 4.
Clue 3: The biggest number for any house in the neighborhood is 15.
Clue 4: The number of the house where Max lives is a multiple of 3.
The Analytical Process of Solving the Mystery
Now that you’ve given yourself a chance to work through the problem, let’s go step by step to understand one way we can think about putting the clues together.
Clue 1: What are the powers of 2 that are greater than 0 and less that 10? They are 1=20, 2=21, 4=22, and 8=23. So we need to take one number from the set {1,2,4,8} and a second number from the same set {1,2,4,8} and add them together to come up with the list of possible house numbers. Remember that both numbers can be the same but do not have to be. We’ll leave the arithmetic to you, but we should all arrive at the following possibilities:
Clue 2: Although we don’t yet know any of the house numbers in the arrow diagram of the neighborhood, what can we figure out from the information given? One thing is the location of the house with the smallest number. It has to be the house at the bottom of the picture because the arrows tell us that every time you go from that house along either of the two roads, you add 3 or 4 each time. So you keep getting bigger and bigger house numbers, and they never fall back below the number you started with at the bottom, whatever that number is.
Likewise, is there anything we can say about the largest house number in the neighborhood? Well, it’s probably at the top of the diagram since the house numbers get bigger as you go up the roads. But is it the house on the top left or the one on the top right? Now we need some variables now to help us keep track of these houses.
Let’s call the house number at the bottom “A,” the one on the top left “B,” and the one on the top right “C.”
We know B is bigger than A, and C is bigger than A. Can we say anything about how much bigger B and C are than A? Well, to get from A to B, we add 3 and 3 and 4. That is, we add 10 = 3 + 3 + 4. So A + 10 = B. To get from A to C, we add 4 and 4 and 3. That is, we add 11 = 4 + 4 + 3. So A + 11 = C. We’re starting with at same number, A, and adding 11 to get to C but only 10 to get to B, so C must be bigger than B. Now we know that the house with the biggest number is on the top right.
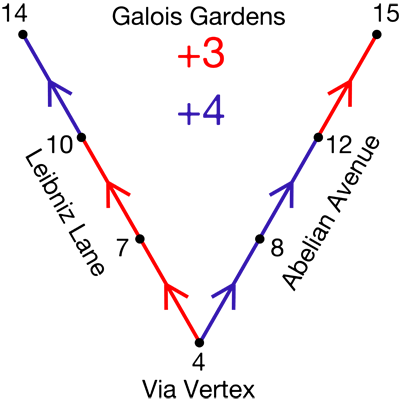
Clue 3: This clue, along with what we figured out from Clue 2, tells us that C = 15. In other words, the address of the house at the top right is 15 Abelian Avenue. With a little arithmetic, we can now determine the rest of the addresses in the neighborhood as follows:
Now that we have all the addresses in the neighborhood, we can go back to our original list of possible house numbers from Clue 1 and cross off the ones that do not show up in the neighborhood. Here’s what our list should look like now:
Clue 4: We’re down to only three possible house numbers—4, 8, and 12. Clue 4 tells us that the house number is a multiple of 3. Which of these possibilities is a multiple of 3? Only 12 is a multiple of 3. Hooray! We figured out where Max lives—12 Abelian Avenue! Sofia will be so happy to have Max back at home, and Emily will be quite pleased with herself for having solved the mystery and done a good deed.
Show a child some tricks and he will survive this week’s math lesson. Teach a child to think critically and his mind will thrive for a lifetime.
Math word problems confound many students for a variety of reasons. Too often, well meaning parents and teachers attempt to help students struggling with these kinds of problems by offering them tricks or shortcuts for getting to the solution without necessarily understanding what’s going on. Just do an internet search for something like “how to solve word problems,” and you will get a slew of Web pages with tips, tricks and strategies like the following:
• Search for key words that will tell you which mathematical operation you should use (e.g., “lost” means subtraction).
• Cross out non-essential information so that you are not distracted by it.
• Draw a picture to illustrate each step of a problem.
Let’s consider these three examples for a moment. To suggest that looking for key words within the text of a math problem is somehow a “strategy” to solving it more easily seems a bit absurd. Basic reading comprehension skills are obviously essential to solving any problem, math or otherwise, where the information is communicated via natural language. No key word mapping is going to provide a fool-proof way of understanding what a word problem is asking. If you’re starting with a word problem that is well designed and written with clarity, there simply is no “trick” to understanding the words.
The other two examples sound reasonable on the surface, but a closer examination reveals problems with them too. To determine which pieces of information are relevant to the solution (as in Example #2), you need to be able to evaluate and analyze the given information. To correctly translate the words of a problem into a step-by-step illustration (as in Example #3), you need to be able to understand and prioritize the information. In other words, tricks like these seem to require the very skills needed to solve the problem without the tricks! Furthermore, a “tip” cannot tell you whether you have enough information to solve the problem, or how to find any missing information. Only critical thinking and logical reasoning skills can help you there.
This approach of relying on “clever strategies” to replace critical thinking runs counter to the IMACS philosophy of teaching children the fundamental skills they need to solve problems throughout their lives, whether they be elementary word problems or complex Calculus problems, whether it’s making correct change or correcting the flight path of an exoplanet-bound space craft.
Meaningful Strategies That Matter
While silly tricks may work for some students as a short-term fix to “just get through the problem,” there are practical and helpful techniques that should be part of any meaningful approach to understanding and solving word problems.
Pay attention to units of measurement. Word problems commonly feature units of measurement. When finding a solution, it’s important to pay close attention to how you are adding, subtracting, multiplying, or dividing amounts in the problem so that you don’t end up combining “apples and oranges.” If you carefully track the units of measurement through each step of your computation, you can compare the units of your answer to what it should be based on the question. This is a good technique to check the reasonableness of your answer rather than one that “magically” solves the problem for you. Here’s an example:
No one would think that the following approach is right
because adding children to cookies makes no sense! The answer requires a relationship in the form of “X cookies per child” – or, more algebraically,
With this in mind, what makes sense is the following:
While we’re on the topic of cookies, here’s another example:
Most people know to do something with ( 4,500 / 3 ) and 5, but what? Looking at the question in the problem, we know that our answer should be in the form of “X cookies.”
What if we set up the equation correctly
but then worked out our answer as follows?
Hmm … 300 cookies per minute per minute? The fact that our answer is not measured purely in cookies as expected tells us that we made a mistake in our calculation.
Use reverse word problems to practice abstract thinking. The process of solving word problems often requires us to connect a real-life situation described in language we know with the abstract version written with variables and equations. As with learning to speak a foreign language, thinking abstractly becomes more natural with practice and regular use, and the earlier you start, the easier it is.
When kids are younger, parents can help them to develop an intuition for abstract reasoning by doing “reverse” word problems in the guise of creative play. Start by writing down an equation such as 7 + ___ = 10. Next, ask your child to imagine a story that goes with this equation. He might say something like, “It takes 10 gold stars to get extra recess, and I already have 7. How many more stars do I need?” For 3 + (8 × 2) = 19, she might say, “When I started robotics, I took 3 introductory classes. Then, I took 2 classes per week for 8 weeks. So, I have taken a total of 19 classes.”
Be sure to keep the level of difficulty appropriate for your child’s math ability. Frustrating him with a computationally hard problem will only defeat the purpose of teaching him to think abstractly.
Word problems can be used effectively to teach important mathematical concepts and to help give real-world context and purpose to what may seem like useless hieroglyphics to some people. But without a firm foundation in critical thinking and logical reasoning skills, a student is sure to be at a disadvantage when trying to evaluate, analyze, prioritize, and synthesize the numerous pieces of information embedded in the narrative. Tips, tricks, and strategies may help at the margins, but there is simply no substitute for genuine understanding.
Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.
In our previous IMACS blog post on modular arithmetic, we introduced the Clock Game as a fun way to teach children about modular addition. Now, we’ll introduce a few variations on the Clock Game that make it more interesting. If you’re not familiar with the Clock Game, we suggest that you first read our introduction to modular addition before adding on with this post. Have fun!
The Double Game
In the double game, there are two pieces at each number at which to play instead of just one.
The game described in our introduction to modular addition can also be played as a “double game.” The only difference is that when playing double games, a player has more choices. For example, if, as a result of a particular move, a player has to place a checker at a number, one of whose circles is unoccupied and one of whose circles is occupied by the opponent, the player has the choice of either taking the opponent’s checker by replacing it with one of his or her own, or placing a checker on the unoccupied circle and leaving the opponent’s checker on the math. Double games, therefore, last longer, since all the available places must be occupied before the game is over.
Kings and Double Kings
Another variation of the games which can make them more interesting involves the use of kings and double kings. Only one place at each number is used in these games. In this variation, if the move requires it, you may place a second checker on top of one of yours already occupying a particular position, thus creating a “king checker.” If you have a king checker already occupying a certain position, then, if the move requires it, you may place a third checker on top of the king, thus making a “double king.” If a double king occupies a particular position, no further checkers may be added to the pile and so the play continues as in the simplest version of the game.
If your opponent would normally land on a place where you have a double king, then that double king cannot be removed, and the opponent cannot place a second checker. The hour hand, however, should still be moved so as to point at the position occupied by the double king even though your opponent could not place a checker there. If, however, your opponent lands on a place where you have a king, then both your checkers may be removed and replaced by one of your opponent’s checkers. The game ends when all of the positions are occupied by at least one checker upon the completion of a turn. This type of game is scored by counting 3 points for each double king, 2 points for each king, and 1 point for each single checker.
Kings, Double Kings and the Double Game
This variation utilizes the rules of the last two sections simultaneously. The first checker of each move must be placed on an unoccupied position, but there may be several choices for the second checker. For example, suppose your second checker has to be placed at “3,” your opponent has a king on one of the positions labeled “3,” and you have a checker (or a king) on the other position labeled “3.” You may either remove your opponent’s king and replace it with one of your own checkers, or you may form a king (or a double king) of your own. In such a situation, you may always choose either one of the two possibilities offered you by the two positions corresponding to the number at which your second checker is to be placed.
IMACS pays tribute to Belgian mathematician and mathematics educator, Georges Papy, who died in Brussels this past November at the age of 91. Georges and his wife, Frédérique, also a noted mathematics educator, were two of the seminal figures in the development of what eventually became the IMACS Mathematics Enrichment curriculum. We are deeply grateful to the Papys for their life’s work on behalf of mathematics students and their teachers.
The Early Years
Georges Papy was born in Anderlecht, a municipality in Brussels, Belgium of not quite seven square miles, on November 4, 1920. World War I had ended just two years before, and the country, which had suffered immensely under four years of German occupation, was still recovering. Against this backdrop and coming of age during the rise of Hitler, it is no wonder that young Georges was a member of the armed underground resistance forces in Belgium during 1941 – 45, serving in particular in the areas of intelligence and action. An educator from the start, he taught clandestine courses to students at the University of Brussels during 1941 – 42, and taught in a clandestine school for Jews during 1942 – 43 in the town of Méan, 50 miles to the southeast of Brussels.
After the end of World War II, Papy earned his doctorate in mathematics (with the highest distinction) from the University of Brussels in 1945, and was granted his advanced teaching diploma by the Science Faculty of the University of Brussels in 1951. After serving from 1949 first as Reader and then as Senior Lecturer at the University of Brussels, he became Professor of Algebra in the Science Faculty in 1956. The year before, he became a member of the prestigious Institute for Advanced Study in Princeton, New Jersey.
Finding His Purpose: Mathematics Education
During the mid 1950s, influential academic mathematicians were leading efforts to improve the quality of mathematics education in France. In parallel with these developments, Georges became deeply interested in improving the quality of mathematics education at the secondary school level, and assumed a position of leadership in Belgium of what became known as the New Math movement. [This was inspired in part by a colloquium organized in 1959 in Royaumont, France, by the agency that in 1963 would become the OECD. A follow-up meeting held in Yugoslavia under the chairmanship of the American mathematician Marshall Stone gave rise to a secondary school mathematics curriculum that was published in Paris in 1961 under the name “Mathématiques nouvelles” (“New Math”).]
Papy’s work in mathematics education would accelerate quickly from that point. In 1961, he founded the Centre Belge de Pédagogie de la Mathématique (Belgian Center for Mathematics Pedagogy). From 1962 onward, Georges was called upon as an expert in mathematics education by several international groups, including UNESCO, IBM, and the OECD. During 1960 – 70, he served as president of the Commission Internationale pour l’Étude et l’Amélioration de l’Enseignement des Mathématiques (International Commission for the Study and Improvement of Mathematics Teaching), and was founding president of the Groupe International de Recherche en Pédagogie de la Mathématique (International Research Group in Mathematics Pedagogy), starting in 1970. Amid this flurry of activity, Papy even found time to serve as Senator in the Belgian government during 1963 – 64.
Modern Mathematics: A Crowning Achievement
During 1963 – 66, with the collaboration of his wife, Frédérique, Georges published the groundbreaking six-volume series entitled Mathématique Moderne (Modern Mathematics), which represented a fundamental reformation of the secondary school mathematics curriculum based upon the unifying themes of sets, relations, functions, and algebraic structures (such as groups).
His mathematical educational interests expanded to include elementary school education. Starting in 1967, under the auspices of the CPBM, Frédérique and an associate taught experimental mathematics classes to six-year-olds. In the years that followed, Papy and Frédérique published several volumes comprising what amount to annotated accounts of these experimental classes and those that succeeded them. The mathematical underpinnings of this elementary school work remained the same as those of Papy’s earlier secondary school work, prominently featuring the use of multicolor arrow diagrams to represent relations and functions.
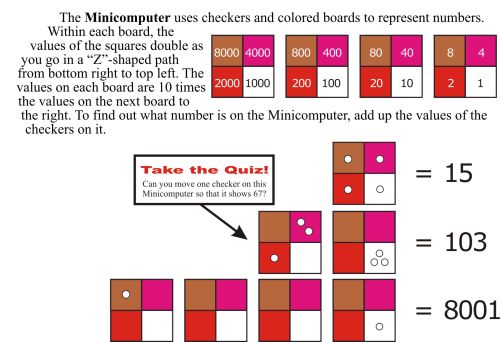
The Papy Minicomputer
As part of this work at the elementary school level, Papy developed what became known as the Papy Minicomputer and published a related text, Minicomputer, in 1968. This is a two-dimensional, mixed binary/decimal abacus made of square boards subdivided into four squares, each color-coded with Cuisenaire rod colors. He attributed the design of the Minicomputer to some work by the renowned Belgian cosmologist Msgr. Georges Lemaître (who was the first to propose what he called “The Primeval Atom” but which Fred Hoyle disparagingly labeled “The Big Bang Theory”). In the mid-1950s, Lemaître had proposed the introduction of new digits to represent numbers. The digits were formed from lines and curves that revealed an underlying binary structure. Papy adapted this idea and transformed it into a two-dimensional board on which checkers may be placed.
The IMACS Connection
In 1969, Georges and Frédérique met IMACS founder Burt Kaufman at the first conference run by the International Commission on Mathematics Education in Lyon, France. At the time, Burt was the director of a federally-funded mathematics curriculum research and development project called the Comprehensive School Mathematics Program. He managed to recruit Frédérique as his Director of Research, a role that she fulfilled during 1973 – 78. Of course, this meant that Georges paid frequent visits to the United States. Consequently, he and his wife had a very significant influence in setting the direction for the development of what has now become the IMACS Mathematics Enrichment curriculum.
Editor’s note: The material below is adapted from ‘Book 0 Chapter 1: Operational Systems’ of the Elements of Mathematics series. The EM series of secondary school mathematics textbooks is a 27-volume collection written and published by the IMACS Curriculum Development Group and serves as a basis for the high-level online math courses available through eIMACS, the distance-learning division of IMACS.
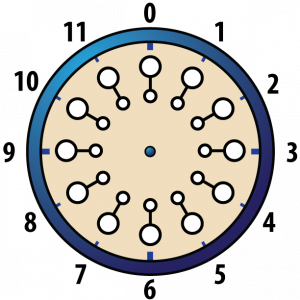
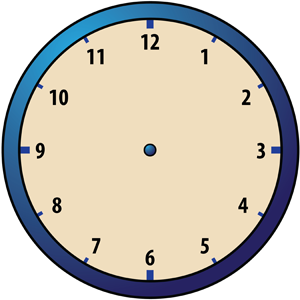
Consider a clock face such as the one shown below:
If the clock shows 10 o’clock, what time will it show 11 hours later? If the clock shows 5 o’clock, what time will it show 12 hours later? If the clock shows 6 o’clock, what time will it show 6 hours later? If you answered 9 o’clock, 5 o’clock and 12 o’clock, respectively, then you’d be right. This exercise suggests a new kind of arithmetic. Let’s call it “clock addition” or, because this kind of addition involves just the numbers 1 through 12, “Clock 12 addition” and denote it by +12. Then the following statements correspond to the three questions above:
10 +12 11 = 9
5 +12 12 = 5
6 +12 6 = 12
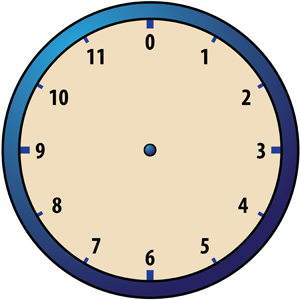
Notice that the number 12 plays a very special role in Clock 12 addition. When you add 12 to any of the numbers from 1 to 12, the number remains unaffected. For example, 5 +12 12 = 5, 12 +12 12 = 12, etc.
In ordinary addition the number 0 has this property. This suggests that it might be convenient to replace the “12” on our clock face by a “0” so that our clock face looks like this:
With this slight change from the usual clock face, we can now summarize the situation as follows: Clock 12 addition involves the twelve numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, and 11. We denote this set of the numbers by Z12 (read, “Z sub 12”). Here is the rule for computing x +12 y for any numbers x and y in Z12.
For all numbers x and y in Z12, x +12 y is equal to:
x + y, if x + y is less than 12, or
x + y – 12, if x + y is greater than or equal to 12
In plain English, that means: To find the Clock 12 sum of x and y, first find the ordinary sum of x and y. If this ordinary sum is less than 12, you are finished – the Clock 12 sum is just the ordinary sum. On the other hand, if the ordinary sum is greater than or equal to 12, then subtract 12 from the ordinary sum to get the Clock 12 sum.
Notice that in any case, as long as x and y are in Z12, x +12 y will also be in Z12. (Can you prove that?) Since for any numbers x and y in Z12, the Clock 12 sum, x +12 y, is again in Z12, we call +12 an “operation” on Z12. Similarly, ordinary addition is an operation on the set of all natural numbers, N, which consists of the numbers 1, 2, 3, … . On the other hand, ordinary addition is not an operation on Z12, and ordinary subtraction is not an operation on N. (What are some examples that support this statement?)
We have been calling +12 “Clock 12 addition” because it’s very closely related to the kind of adding you do on a real clock. The operation +12 is also called “addition modulo 12” or “addition mod 12” for short.
Clock 12 Addition Game
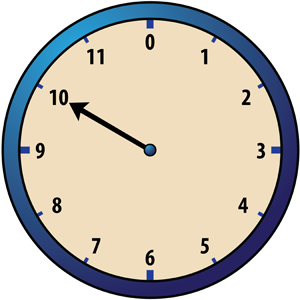
Now we’ll describe a game called “Clock 12” that two players, A and B, can play on a circular board. You’ll need a movable arrow for the hour hand so that your game board looks like the figure below.
Player A begins the game by placing a checker on one of the twelve numbers around the edge of the clock face. The hour hand is placed so that it points at the number on which the checker has been placed. The corresponding time is called “the hour.” For example, if Player A puts a checker on 10, the hour hand is placed so that it points at 10. Player A then says “The hour is 10 o’clock.”
Player B makes a move in two stages: first by placing a checker of a second color on one of the unoccupied numbers, and then by placing a second checker of the same color in such a way that the following is true: The starting hour plus (mod 12) the number of hours corresponding to Player B’s first checker is equal to the time corresponding to Player B’s second checker. The arrow is then made to point at the number on which Player B’s second checker was placed, thus indicating the new hour. Player B then declares the new hour.
Example 1
Suppose Player A begins the game by placing a checker on 10. Then the hour is 10 o’clock. If Player B chooses 4, then his or her first checker is placed on 4, and the second checker is placed on 2 because 10 +12 4 = 2. The hour hand is then moved to 2 o’clock.
Example 2
Suppose Player A chooses 0. If Player B chooses 4, the first checker is placed on 4. In this case, 0 +12 4 = 4, and Player B already has a checker on 4. Therefore, there is no need to place a second checker on 4, and so Player B’s turn ends with the hour being 4 o’clock.
Example 3
Suppose Player A chooses 10 and Player B chooses 0. Then, since 10 o’clock plus 0 hours is 10 o’clock, Player B’s second checker ought to be placed on 10. However, Player A’s checker is already on 10. In this situation, Player B takes Player A’s checker and replaces it with one of his or her own. The hour hand, which was pointing to 10 before Player B’s move began, will not be changed. The hour is still 10 o’clock.
The players continue to alternate turns using rules described in the examples above. If, after completing his or her turn, a player leaves the board so that there are no more unoccupied numbers, then the game is over and the player with the most checkers on the clock wins!
The benefits of math competitions are well known: focusing on goals, dealing with pressure, learning teamwork, and building friendships are among those typically mentioned. Math competitions also allow for the much needed celebration of intellectual achievement the way athletic achievement has always been celebrated. At IMACS, many of our math enrichment students enjoy competing in the American Mathematics Competitions, International Mathematical Olympiad, and MATHCOUNTS among other contests, so we have a very positive view of math competitions, particularly for the kids who thrive in that environment. We’re extremely proud of our numerous students over the years who have performed well in these prestigious contests. We’re equally proud of our numerous students over the years who have thrived in quiet contemplation.
This brings to mind an article published last week by The Wall Street Journal on the challenges encountered by Type A parents raising Type B kids. The article talked about different ways that ambitious, competitive, and hard-driving parents modify their interactions with or expectations of their dreamy, mellow, and seemingly laid-back children to foster healthy parent-child relationships. Whether Type A or not, most parents are cognizant of today’s ultra-competitive global environment, and many feel a sense of urgency to nudge, push, or even pressure their kids to achieve. It’s not a stretch to imagine the parents of a mathematically talented child thinking, “If all the other kids are involved in math and science, then my child should be doing even more.” Here’s the thing: What makes an activity suitable for even more depends on what works for your child and is not necessarily the same activity enjoyed by all the other kids but with more time dedicated to it or with better results.
For parents considering activities for their mathematically talented child, it is important to understand how innate personality factors into the mix that determines whether math contests provide a net positive experience for that child. Just as there are natural-born competitors among mathematically talented students, there are also natural-born dreamers. These kids used to get a bad rap for being unfocused, undisciplined, and even lazy. There was no observable productivity associated with daydreaming so, of course, it had to be a waste of time. Not so fast. In 2009, researchers from the University of British Columbia published a study in the Proceedings of the National Academy of Sciences detailing that brain activity increases when our minds wander. Reporting on this finding, ScienceDaily.com put it well: “[B]rain areas associated with complex problem-solving – previously thought to go dormant when we daydream – are in fact highly active during these episodes.” And from The Wall Street Journal: “These sudden insights … are the culmination of an intense and complex series of brain states that require more neural resources than methodical reasoning.”
If your child is more of a dreamer (or just not drawn to competition), activities that would cultivate his or her talent in and appreciation for mathematics may differ from what is offered through a typical regional, national, or international math contest. Students of this personality type often find more success and satisfaction with math enrichment programs that focus on deep problem-solving over computational prowess. This is not to say that your child shouldn’t at least try participating in some type of competitive math. The experience just might open up a different side of his or her mathematical personality. In fact, our math enrichment classes use game-playing and mini-competitions as teaching tools, and most of our students really enjoy this aspect of the class the best. But if it’s clear that competition does not bring out the best in your child, we encourage you to explore other options including letting your child have more free and unstructured time to let his or her mind ruminate about the wonders of mathematics.
For parents of talented children, the secrets of mathematical success are really not that different from general advice on positive parenting. They include understanding what kind of child you have, knowing what motivates him or her, and fostering an environment that includes the kind of math activities or, quite possibly, freedom from structured activities that align best with that motivation. And if having a dreamer for a child still makes you worry, just think about the great mathematical and scientific discoveries we owe to dreamers of the past. You never know what grand ideas are simmering behind those eyes staring off into the distance.
Dreamer Matching Puzzle
We made a simple matching game out of the Wall Street Journal article that reported on the aforementioned University of British Columbia study. See if you or your kids can match the great thinker with his profound idea and what he was reportedly doing at the time moment of insight. Answers may be found in the article.
Great Thinker: (A) Archimedes, (B) Newton, (C) Einstein, (D) Descartes, and (E) Tesla.
Profound Idea: (1) special relativity, (2) coordinate geometry, (3) alternating electrical currents, (4) calculating the volume of an irregularly shaped object, and (5) law of universal gravitation.
Dreamy Activity: (i) lying in bed watching flies on the ceiling, (ii) taking a bath, (iii) watching an apple fall from a tree in an orchard, (iv) taking a walk, and (v) imagining trains and lightening.
Editor’s note: Regular readers of this blog will notice a slight change going forward. IMACS will be switching to a bi-weekly publishing schedule with our next post appearing on November 10, 2011.
« Newer Posts