• Information for Parents
• Information for Students
• Information for Educators

The above quote comes from a recent article by Stanford professor Jo Boaler. Professor Boaler, through her Youcubed organization, advocates for valuing depth and creative problem-solving over computational speed and memorization in K-12 math education. She further argues that classroom emphasis on the latter is partly to blame for the poor understanding and dislike of math in the US and the unfortunate belief by some students that they are not "math people."

How did the US get to a place where so many people think that math achievement is indicated by a limited and limiting set of skills? Would you really measure achievement in literature or composition by how well and quickly a student spells and punctuates? Of course not! Language arts subjects are accepted as a form of art with all of the associated depth, creativity, and multifaceted approaches to thinking. Although genuine mathematics shares these characteristics, for decades school math has typically skimmed the surface of math knowledge, allowed little room for creative thinking, and focused on the "right" way to get the answer.

While math assignments are constructed and graded rather narrowly, language arts assignments are regularly assessed for creativity and style in addition to technical proficiency. But did you know that professional mathematicians also place a high value on creativity and style when it comes to reviewing each other’s work? Clever and elegant proofs are admired far more because they unveil and illuminate the inherent beauty in mathematics in ways that technically correct but unwieldy proofs cannot.

At the K-12 level, an educator skilled in mathematical thinking can teach even the youngest students the kind of rich mathematics that inspires creative problem-solving and a genuine love of learning. It is these skills, not computational speed and memorization, that will better prepare students for success in the modern world.

This month’s IMACS Blog features Shiva Oswal, one of the top performers in our Elements of Mathematics: Foundations (EMF) self-paced, online program for talented secondary school students. Shiva has been enrolled in EMF since the beginning when IMACS introduced the first course of the series in late 2012. As his mom told us, “[O]ur son is an avid user of online educational resources. I recently asked him to pick his favorite online course. He answered, ‘most definitely EMF, by a wide margin’.”

Please tell our readers a little bit about yourself and what you enjoy doing.

I’ll be turning 11 soon, and I love the EMF courses! As a history buff, I really enjoy reading about decisive battles in world history. I also like playing board games and computer games. Right now my favorite board game is Robo Rally, and my favorite computer game is Castle Empire. On the weekends, I participate in Live Action Role-Playing (LARP) events. Soccer is another activity I enjoy. My favorite position is goalie.

You’ve done some amazing things already at a young age. Tell us about the accomplishments of which you are most proud.

This year, I scored 24 out of 25 to earn a gold pin in the Mathematical Olympiads for Elementary and Middle Schools (MOEMS), and was named MOEMS “Mathlete of the Year” for my geographic region. I also invented a new board game called “Minetrap”. I am currently working on publishing my game. If you would like updates, email me at shivarasul [at] gmail [dot] com. Finally, I completed the first seven EMF courses and am almost finished with the eighth course. I am excited to start the ninth course, Number Theory soon.

How did you become interested in mathematics?

When I was in preschool, I was doing multiplication. When math in regular school became too easy, I decided to homeschool so I could work on challenging math problems and concepts.

How did you become interested in taking EMF courses?

My mom encouraged me to try the EMF courses, and I’ve been hooked ever since.

What are the things you enjoy most about EMF?

I like the way concepts are explained. The format of EMF courses, reading followed by exercises, helps check my understanding. The interactive tools such as The String Game make learning math fun. Also the point system (i.e., ability to level up based on mastery of material) makes EMF addictive.

What are some ways in which your EMF experience has had a positive effect on your academic and non-academic pursuits?

When I did my first EMF course, Operational Systems, I was very new to the field. I learned a great deal about operational systems and modular arithmetic after I completed this course. I have grown by leaps and bounds as an analytical thinker as EMF courses force me to think. The program has also helped me improve my skills at strategy games like chess.

What kinds of things do you see yourself doing in the future?

First and foremost, I would like to complete all 15 EMF courses. I hope to get to Calculus before I’m 13 years old. I am also working on becoming a professional soccer player.

Thank you, Shiva, for sharing your story and congratulations on your amazing accomplishments!

Discover why the Elements of Mathematics: Foundations program from IMACS is an excellent option for your mathematically talented middle-school-aged child.

Bundled Savings: Save 25% on EMF Course Pack 9, which includes the first nine courses, when you enroll on or before December 20, 2014.

Tomorrow is Halloween! Whether it’s watching a horror movie or jumping out from behind a door, many people find it fun to be scared or scary on this holiday. It’s also a good time to revisit what parents can do to keep their children from becoming afraid of math. Math anxiety is unnecessarily common in the United States. As a country we have focused intentily on promoting foundational literacy skills, but numeracy skills can also be fostered from an early age. At home, don’t just read to your toddler and pre-schooler; “math” to them also. Get down on the floor with your kids and some blocks to show them what “more” and “less” and different numbers actually mean. Make patterns out of just about anything age-safe such as different color socks or whole fruits and vegetables. When your kids are around 5-6 years old, playing with coins (counting and adding pennies, exchanging coins, etc.) on the floor is another fun activity.

Math outdoors is fun too! Go to the park and arrange rocks or wood chips into rows and columns. Draw shapes in the sandbox. Are there shapes that look the same no matter where you stand? Which shapes look like they’ve flipped or turned? Make shapes out of sticks. Compare the sticks. Which is longer? Which is shorter? Add sticks to go from a triangle to a rectangle to a pentagon and so on. If you keep adding sticks, what does your shape start to look like? (Don’t freak out, but you just did a little Calculus.)

Good old-fashioned floor time or outdoor time are excellent ways of cementing learning with positive memories. As your kids get older, make sure they are exposed regularly throughout their childhood and adolecense to adults who explain math well and enjoy it, especially if you don’t. And if you have math anxiety yourself, make that your best-kept secret. Math doesn’t have to be scary.

Now, what do you get when you take the circumference of a jack-o-lantern divided by its diameter? Answer: A pumpkin π. Happy Halloween from IMACS!

Once upon a time, there was a bright student who first came to IMACS when he was already in high school. He was interested in learning to program and had heard high praise for our University Computer Science courses. The class began smoothly as teacher and pupil progressed through the principles of computational thinking. This student, who was used to conquering schoolwork with his brain tied behind his back, slayed the early exercises with ease. As the assignments quickly became more challenging, however, he found himself unaccustomed to the effort of intellectual struggle. One day, our earnest student declared to his IMACS instructor that a certain programming problem was simply impossible to solve! Our wise and experienced teacher considered this student with a measured gaze and pointed out, “But you’ve only thought about it for three minutes.” The student, quite politely, seriously, and honestly replied, “Well, yeah.” If only he had started IMACS when he was younger. The moral of the story: The earlier the experience of true intellectual challenge, the stronger the will of the mind to persevere. (In other words, enroll your elementary school child in IMACS today!)

This month the IMACS Blog caught up with Azzara Nincevic, who has been a star student at IMACS for seven years now. Azzara enjoys reading, drawing, and classical ballet. Although she dances at least 12 hours per week and performs throughout the year, she always finds time for IMACS.

“When I began IMACS in first grade, I immediately loved it.” Azzara says. “Having taken an interest in math, I quickly learned the traditional material and was looking for more challenging enrichment. When I attended class at IMACS, all of the problems were thought-provoking.”

As a member of her school’s math team, Azzara attends competitions such as MATHCOUNTS and Mu Alpha Theta where her IMACS background has been an invaluable asset. As Azzara describes it, “The IMACS curriculum helped me to develop logical thinking skills and the ability to quickly solve math problems, which are key to succeeding at math competitions.”

While Azzara’s achievements in mathematics and ballet, by themselves, are enough to impress anyone, it’s her recent performance on the AP^® Computer Science A exam that readers will recognize as a rare feat. Soon after starting IMACS Math Enrichment program, Azzara enrolled in our Computer Enrichment & Virtual Robotics class where she developed a great interest in programming. Over the years, she continued with IMACS University Computer Science (UCS) track, which culminates in our AP^® Computer Science: Java Programming course.

AP^® exams are typically administered to high school students, but at the time that Azzara was ready for APCS, she was only just entering seventh grade. That didn’t deter her. “After inquiring, my mom and I found out that there is no minimum age requirement for an AP^® exam, so I registered. With the preparation that IMACS gave me, I was able to score a 5 on the AP^® Computer Science exam as a seventh grader.”

With such a busy schedule, Azzara appreciates that one of the greatest benefits of IMACS is that the computer science and logic programs are accessible online and self-paced. “I was able to excel at my own pace and access the IMACS curriculum anytime and anywhere.”

What does the future hold for Azzara? “I am entering the eighth grade with a greater passion for and interest in math and computer science. IMACS made me realize that I would like to pursue computer science in college and after. The fundamental skills that I have learned in the UCS courses and the logical thinking skills I have learned in the Math Enrichment and Mathematical Logic courses give me the advantage I need to be successful. As such, I plan to continue with IMACS in the upcoming years.”

If you’re not planning on pursuing a so-called STEM career, do you really need to be good at math? Yes, but not just for the often-stated reason that people encounter math regularly throughout their lives. Being able to handle everyday math is certainly important. For example: If you’ve been offered varying aid packages by different universities, which one makes the most financial sense for your family? If you’re deciding between leasing or buying a car, which is the best deal in the long run? While no one doubts that being better at money arithmetic would benefit individuals and society as a whole, such specific situations require a narrow skill set.

The benefits of being good at math, however, go beyond correctly computing the tip at dinner to a wide array of circumstances that call for abilities prized in virtually every field of employment. For example, people who have learned to think mathematically are better at understanding the structure required to complete a given task. The first step in solving any math problem is sizing up the situation. What do you already know? What information is missing? Can you break the larger problem into more manageable pieces? Having both the skills and confidence to dissect complex problems, including ones that look nothing like what you’ve seen before, is one of the main benefits of becoming good at math.

People who have learned to think mathematically are also better at assembling new ideas. Once you’ve assessed the situation, broken down the problem, and gathered the necessary pieces, how do you put it all together to get from where you are to where you want to be? When faced with a novel situation, can you devise an approach where there wasn’t one before? If you’ve studied mathematics in a way that pushes you to think both logically and creatively, then you will be much better prepared to handle an ever-changing variety of circumstances that call for these skills, no matter what career you choose.

Broward County, Florida students currently attending grades 6-8 are invited to apply to the IMACS Math Academy, an intensive one-week program designed to stimulate talented students’ interest in mathematics beyond the traditional classroom. There is no cost to attend the IMACS Math Academy!

There are two scheduled sessions. The first will be held March 24 – 28 during Spring Break. The second will be held June 23 – June 27 during Summer Break. Both sessions of the IMACS Math Academy will be held at IMACS Headquarters in Plantation, Florida.

To be considered for one of the two available sessions, students must first complete an online aptitude test by February 28, 2014. Up to 60 students who do well on the aptitude test will be invited to apply to the IMACS Math Academy.

Parents interested in the IMACS Math Academy should visit www.imacs.org/mathacademy.

The following letter is extracted from the new book, Letters to a Young Math Teacher, by Gerald Rising and Ray Patenaude, which is available from Amazon.com and other sources. Gerry Rising is Distinguished Teaching Professor Emeritus at State University of New York at Buffalo where he co-founded the university’s Gifted Math Program for highly-qualified regional students in grades seven through twelve. Gerry Rising was for many years associated with IMACS activities and is a strong supporter of our work.

Paul Rosenbloom enjoyed an international reputation as a senior mathematician when I joined his Minnemath Project at the University of Minnesota as his assistant director. His Elements of Mathematical Logic remains today a basic resource recognized worldwide to be of historical as well as academic significance.

In our very first conversation he told me that he considered teaching outside the classroom an important aspect of a mathematician’s life and he urged me to develop what he called “a bag of tricks” from which to draw math-related lessons for people of all ages. I would later see him draw from his own collection in a number of settings. He could captivate anyone from nursery school students to scientific colleagues and even senior political figures.

Within a month of that conversation I found myself seated on an airplane flying from Minneapolis to Denver. My seat partners were a bored nine-year-old and her mother. When the mother learned that I was a math teacher, she asked me if I would be willing to “show Marjorie some math.”

Fortunately, I had been reading David Silverman’s book, Your Move, and I had some pennies with me. I played a series of Nim games with Marjorie, finding her an interested opponent and a remarkably quick study.

Nim, for readers unfamiliar with the word, is German for “take” and in this context it applies to games with players taking one or more counters like coins from a collection following a given set of rules.

We started with One Pile Nim. I set out a line of pennies on Marjorie’s tray and explained the rules. We would take turns, at each turn removing one, two or three coins. The winner would be the player who could take the last penny or pennies.* When she quickly determined the strategy for playing, I suggested she challenge her mother. Her eyes lit up as she outplayed her mom.

Now she wanted more. I suggested the misère form of the game: same rules for play but this time the loser forced to take the last coin. Now I had her mother’s full attention as well, but again Marjorie, once she found the winning strategy, could outplay mom.

We went on to play the very simple Two Pile Nim game in which each player takes any number of coins from one of two piles with the winner taking the last coin, but then the less transparent game, Woolworth, which is isomorphic to Two Pile Nim. Woolworth is named for the five-and-ten-cent stores of the 1950s that have been reincarnated as today’s Dollar Stores. On a sheet of paper I drew the following diagram:

I placed nickels and dimes as shown in the figure. One player controls the coins on the left, the other the coins on the right. Players alternate moving either of their coins any number of squares to left or right but without joining or passing the opponent’s coins. The object of the game is to squeeze your opponent so that no moves remain.

By the time I showed Marjorie the connection between Two Pile Nim and Woolworth we were well on our descent into the Denver airport. I was rewarded for our hour together when Marjorie turned to her mother to tell her that she wanted to become a mathematician.

Where do you find lessons like these that require no background and yet are suitable to given age groups? I found mine from two sources: my reading of journals and books about mathematics and my observation of lessons taught by others. Appendix 2 lists a few of the many available book sources.

Now, because it is a good story, I will tell you about my use of a lesson copied from the remarkable teacher, Robert Wirtz.^

Late one school year when I was a math supervisor I was asked by a primary school teacher to demonstrate Stern blocks for her students. Stern blocks are inch cross-section blocks that come in lengths from one to ten inches. Cuisenaire rods are similar but with centimeter dimensions.

I took several sets of Stern blocks to this teacher’s classroom and showed the six-year-olds some of the relationships among them.

The students were excited by the opportunity to mix play with learning, and I was convinced that they were gaining from the lesson. I noticed, however, that their teacher was not happy with the children’s mix of play with learning. Several times she interrupted their activities to tell individuals to be quiet.

It was clear to me that the teacher was convinced that I wasn’t disciplining the children in the way she wished, so I suggested that I return the next day to teach another lesson. Despite her reservations about my conduct of this class, she jumped at the chance to have me return. It was clear that she was happy to pass responsibility for these irrepressible kids off onto anyone she could find.

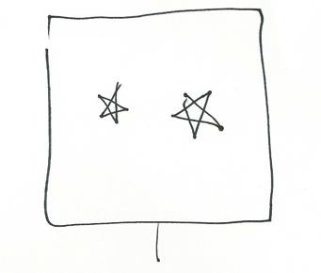
I had seen Bob teach a lesson to a similar group and the next day followed his model. Before the class I had the teacher gather the students in front of the chalkboard. Saying nothing to them I drew a square on the board and within it marked two star shapes. What I had drawn looked like this:

I pointed to that little tail at the bottom of the figure and turned to the class, holding out the chalk.

Several hands waved and I offered the chalk to one of the wavers. The boy came up and carefully wrote a “2” below the diagram.

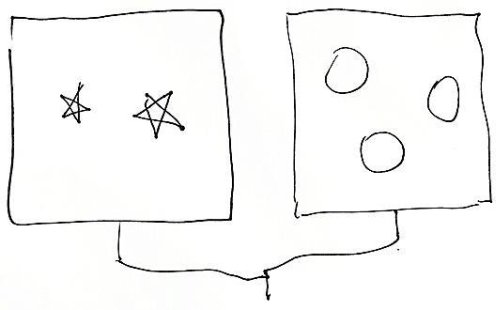
That got us started. I drew similar diagrams with different shapes and the children quickly caught on, competing to write the numbers below the figures. Then I began to complicate the requests by erasing their numbers and connecting two figures like this:

No problem. A volunteer wrote “5” below the boxes.

I continued in this fashion, soon replacing the boxes with numbers but using the same connecting segments. All of the children were eagerly participating, but not one word was said by me or by any of them.

After a half hour of this activity, I finally spoke up, calling the children’s attention to the fact that none of us had spoken until then. And I turned to their teacher to congratulate them on what we had accomplished.

Unfortunately, my lesson proved nothing to this young woman. Her response: “Yes, after you left yesterday I really scolded them for their behavior and you saw the result this morning.”

Even with the best of efforts, you cannot always win.

I have talked about these mathematical extras mostly in terms of their use outside of your classroom, but they can play a role in your classes as well. Here is an example described by Swedish math educator Barbro Grevholm:

Please take the examples I have used only as samples of my own and others’ collections of activities. You may or may not add them to your collection. What is important is that you accumulate such activities that work for you. They will serve you well.

Sources of such activities are all around you. You just have to be alert to them and adapt them creatively.

Many such activities come from your reading. Mathematics and mathematics education journals describe topics and lessons that you can both enjoy and share with others. Of course, you should credit your source when you replicate such a lesson, but every writer I know would be delighted to know that his or her lesson was being duplicated.

The two best journal sources I know for such examples are the Mathematical Association of America’s Math Horizons and the British Mathematical Gazette.

Some non-standard texts are full of such lessons. Authors like Harold Jacobs and Sherman Stein are two who have gathered and present such useful topics. And some authors simply collect such presentations. Among these are Ian Stewart, Ross Honsberger and Howard Eves.

In a class by himself is Martin Gardner whose collections of such topics are unsurpassed. His range is amazing, covering everything from hexaflexagons to fractal music, almost all of them serving a perfect basis for well-planned demonstrations.

Even your daily newspaper can provide activities. Although many people are drawn to the Sudoku puzzles, I much prefer three other popular forms: Kakuro, KenKen and Numbrix. These puzzels are adaptable to students of all ages (I solve one or two each day) and can challenge them all. The simplest appearing is Marilyn vos Savant’s Numbrix. While this puzzle task is appropriate for primary grade students (all it involves is listing the integers from 1 to 81 in order in a 9×9 grid), individual Numbrix puzzles range widely in difficulty.

In addition to their intellectual challenge, there are two things about the Kakuro and KenKen puzzles that I find attractive: (1) they involve basic calculation facts that reinforce the solver’s skills and (2) they appear as free apps on mobile phones and tablets. This availability makes them perfect puzzles to introduce to fellow travelers.

* The strategies for playing these Nim games are included in Appendix 4. I encourage you to play the games before you look at those strategies.

^ Bob Wirtz and his wife adopted a number of children with severe learning problems and they developed math materials to teach them. With Mark Botel, then president of the International Reading Association, he gathered those materials into books for elementary school students. Sadly, they are difficult to find today for they include some very attractive activities.

UPDATE, May 27, 2014: IMACS student, Peyton Robertson, impressed President Barack Obama at today’s fourth annual White House Science Fair. Watch Peyton with President Obama starting around the 4:35 mark of this video.

UPDATE, October 9, 2013: Congratulations to IMACS student, Peyton Robertson, on winning the title of “America’s Top Young Scientist,” $25,000 and a trip to Costa Rica! Watch Peyton’s winning moment.

From the moment you meet IMACS student, Peyton Robertson, you can’t help feeling that he is one of those bright, young people who is going to leave his mark on the world in a big way. His creative ideas and energy seem boundless. His smile and enthusiasm are infectious. And he’s just 11 years old!

Most recently, Peyton entered the 2013 Discovery Education 3M Young Scientist Challenge and is one of only 10 finalists (and the youngest) in this prestigious national science competition for 5th through 8th graders. The Young Scientist Challenge encourages students to explore science and innovation during the pre-teen years when interest in math and science typically starts to decline.

Peyton’s project, SOS: Sandless Operational Sandbags, focuses on developing a more effective and less costly sandbag design to protect against damage from saltwater flooding. As Peyton notes in his finalist video, 80% of the $43 billion dollars worth of flood damage caused since 2005 has been from saltwater flooding. Peyton’s native Florida is at risk for hurricane-driven saltwater flooding every year. So he’s decided to do something about it by re-engineering the basic tool of flood control: the sandbag.

The design of traditional sand-filled sandbags means that they are heavy, difficult to transport and, when stacked, leave gaps through which water readily flows. Peyton’s design uses a thin, expandable polymer to keep his bags light and easy to transport. He also pre-fills his bags with enough salt so that when it dissolves, the salt content of the solution inside is higher than that of seawater, helping to keep the seawater from penetrating the bags. Finally, Peyton uses an ingenious interlocking design to minimize the gaps between the bags when they swell. When the water recedes and the bags dry out, they return to their thin, easily transported and stored form, ready for use during the next storm.

IMACS is so proud of Peyton and delighted to count him as one of our many exceptional students. When we asked Peyton’s mom, Shannon Robertson, to describe the influence that IMACS has had on his education, this is what she had to say:

Congratulations, Peyton! Your friends at IMACS wish you the best in the finals of the 2013 Young Scientist Challenge.

The Institute for Mathematics and Computer Science (IMACS) is pleased to announce Elements of Mathematics: Foundations, a new series of online courses designed for bright secondary school students. EMF is a self-contained program that allows the talented student to complete all of middle and high school mathematics up to Calculus before leaving middle school. The curriculum is the result of more than a decade of research and development by an international team of mathematicians and educators and has been in use with gifted and talented students for over 20 years.

Acceleration vs. The EMF Approach

For mathematically talented schoolchildren, subject acceleration is an oft-advised tool for addressing their need to learn more challenging material. Through subject acceleration, a student works on math curriculum that is normally taught at a higher grade level. While acceleration does help bright students avoid repetition of material in which they are already proficient, by definition it cannot help them avoid the tedium that is the standard US mathematics curriculum.

EMF is not an accelerated version of the standard US mathematics curriculum. Instead it provides a deep and intuitive understanding of foundational concepts. This allows the suitably talented child to progress quickly through material for which others would require significant drill and practice. The curriculum then proceeds to cover concepts in a mathematically consistent way, going well beyond the typical gifted math class offered in schools or online. Topics from the standard curriculum – and much, much more – are taught in an intellectually engaging way.

Six Ways In Which EMF Is Unique

• The EMF curriculum was designed from scratch specifically for gifted and talented children to leverage their advanced capacity for learning and to engage their unique ways of thinking.

• EMF provides a deep, intuitive, and lasting understanding of mathematics as a cohesive body of knowledge that opens the door to scientific discovery and technological advancement.

• EMF focuses on the powerful and elegant ideas of mathematics, the kind that gifted and talented children find deeply satisfying and inspiring.

• The EMF curriculum exposes students to subject areas not found in the standard curriculum such as operational systems, set theory, number theory, abstract algebra, and probability and statistics.

• EMF maintains a level of mathematical rigor found typically at the university level while making advanced concepts accessible and fun for a younger audience.

• EMF gives students a true sense of what it takes to excel in college math courses, which is not the same as the skills needed to do well in standard math classes or at math competitions. EMF students do not have to “unlearn” certain habits before they can move forward with more rigorous math courses.

Is EMF Right For Your Child?

EMF courses are self-study and require a certain level of intellectual maturity. Talented students who have completed all of elementary school math but have not yet completed algebra and geometry would gain the most from EMF. However, students who already have some experience of algebra and/or geometry may still find benefit because EMF introduces concepts that are not covered in standard high school mathematics classes.

Parents who register their child at www.elementsofmathematics.com will be offered the option of having their child take a free online aptitude test to help determine their child’s level of readiness.