• Information for Parents
• Information for Students
• Information for Educators

The Institute for Mathematics and Computer Science (IMACS) is pleased to announce Elements of Mathematics: Foundations, a new series of online courses designed for bright secondary school students. EMF is a self-contained program that allows the talented student to complete all of middle and high school mathematics up to Calculus before leaving middle school. The curriculum is the result of more than a decade of research and development by an international team of mathematicians and educators and has been in use with gifted and talented students for over 20 years.

Acceleration vs. The EMF Approach

For mathematically talented schoolchildren, subject acceleration is an oft-advised tool for addressing their need to learn more challenging material. Through subject acceleration, a student works on math curriculum that is normally taught at a higher grade level. While acceleration does help bright students avoid repetition of material in which they are already proficient, by definition it cannot help them avoid the tedium that is the standard US mathematics curriculum.

EMF is not an accelerated version of the standard US mathematics curriculum. Instead it provides a deep and intuitive understanding of foundational concepts. This allows the suitably talented child to progress quickly through material for which others would require significant drill and practice. The curriculum then proceeds to cover concepts in a mathematically consistent way, going well beyond the typical gifted math class offered in schools or online. Topics from the standard curriculum – and much, much more – are taught in an intellectually engaging way.

Six Ways In Which EMF Is Unique

• The EMF curriculum was designed from scratch specifically for gifted and talented children to leverage their advanced capacity for learning and to engage their unique ways of thinking.

• EMF provides a deep, intuitive, and lasting understanding of mathematics as a cohesive body of knowledge that opens the door to scientific discovery and technological advancement.

• EMF focuses on the powerful and elegant ideas of mathematics, the kind that gifted and talented children find deeply satisfying and inspiring.

• The EMF curriculum exposes students to subject areas not found in the standard curriculum such as operational systems, set theory, number theory, abstract algebra, and probability and statistics.

• EMF maintains a level of mathematical rigor found typically at the university level while making advanced concepts accessible and fun for a younger audience.

• EMF gives students a true sense of what it takes to excel in college math courses, which is not the same as the skills needed to do well in standard math classes or at math competitions. EMF students do not have to “unlearn” certain habits before they can move forward with more rigorous math courses.

Is EMF Right For Your Child?

EMF courses are self-study and require a certain level of intellectual maturity. Talented students who have completed all of elementary school math but have not yet completed algebra and geometry would gain the most from EMF. However, students who already have some experience of algebra and/or geometry may still find benefit because EMF introduces concepts that are not covered in standard high school mathematics classes.

Parents who register their child at www.elementsofmathematics.com will be offered the option of having their child take a free online aptitude test to help determine their child’s level of readiness.

In our previous IMACS blog post, we began our response to Professor Andrew Hacker’s op-ed piece entitled “Is Algebra Necessary?” by taking a critical look at his reasoning in favor of eliminating the requirement for high school algebra. We argued instead that the approach to teaching algebra, and more broadly all of mathematics, should be changed significantly in the US to benefit all students, from those who are struggling to ones who are at maximum achievement under the current limited system. In this week’s post, IMACS discusses key elements that we believe should be part of any effective curriculum in mathematics.

We were pleased to see that Prof. Hacker quoted mathematics professor Peter Braunfeld of the University of Illinois as saying, “Our civilization would collapse without mathematics.” Prof. Braunfeld is not new to the mathematics education debate, having co-authored an article* on the subject with IMACS principal founder, Burt Kaufman, and IMACS curriculum contributor, Professor Vincent Haag, nearly 40 years ago. (Prof. Braunfeld was also a contributor to the IMACS curriculum.) Their article outlined five principles that have and continue to guide IMACS in our curriculum development.

Everything Old is New Again

A 40-year-old article!? How can that be relevant now? Sadly, the circumstances lamented then by the co-authors remain a plague on our US math curriculum to this day. Have you heard anything like the following excerpts lately?

It’s no wonder that students find math dull and tedious. The trivialized curriculum forced upon them has been stripped of all the wonder and beauty of mathematics.

In just the past year, the articles we’ve read suggesting that video tutorials, massive open online courses, and the iPad are going to “revolutionize” education are too many to count. The drive-thru window may have changed how Mickey D’s was served, but the stuff in the paper bag remained of questionable nutritional value for a long time. (Yet even the Golden Arches eventually overhauled its menu!)

Can we say teach to the test? The idea of “industrialized education” came about long before No Child Left Behind. What’s unfortunate is that such an ill-conceived notion wasn’t what was left behind.

Five Guiding Principles of Mathematics Education

So what are the five guiding principles that the co-authors proposed? The excerpts that follow summarize how they believed mathematics should and can be taught to children and how IMACS teaches today:

Exasperated students continue to ask when they are ever going to need high school math in the real world, and who could blame them? Yet you never hear such broad and fervent protest about high school science even though relatively few kids will put that knowledge to work. Why less complaining? Because science curricula, for the most part, still incorporate grand ideas that elicit awe in young minds. Why are parents appalled by cuts in the arts at school? Not because most think their kids will pursue careers in creative fields, but because they understand that the aesthetic experience lifts the human spirit.

Mathematics is brimming with this kind of elemental beauty too. Yet decade after decade, schools use curricula that deprive math students of the good stuff. It’s like feeding the cardboard box instead of the cereal to a kid and saying “See, it says ‘cereal’ right there on the label. How can you say it’s tasteless?” Children have been telling us for too long that we need to change the menu. It’s time we listen.

*”Mathematics Education: A Humanist Viewpoint,” Braunfeld, Peter, Burt A. Kaufman, and Vincent Haag, Education Technology, November 1973.

Editor’s Note: IMACS will soon be rolling out a series of interactive online math courses designed with the five guiding principles discussed above. These courses will allow talented students to complete all of middle and high school mathematics with the exception of calculus before leaving middle school. Check back at www.eimacs.com or like us on Facebook for exciting details to come!

Andrew Hacker, emeritus professor of political science at Queens College, City University of New York, recently wrote an op-ed piece in The New York Times entitled “Is Algebra Necessary?” His opinions caused quite a stir in the ongoing debate over mathematics education in the US. IMACS sees value in some of his ideas, such as teaching quantitative reasoning starting in kindergarten, and we agree that schools should not subject students to the “ordeal” of struggling with algebra. However, IMACS believes that education professionals should focus on changing the way mathematics is taught, not on eliminating the requirement to study algebra.

First, consider the attendant consequences of the author’s proposal, which is to create alternative math courses that “familiarize students with the kinds of numbers that describe and delineate our personal and public lives.” Perhaps the large yet still minority percentage of students who cannot pass traditional algebra would be allowed to satisfy their high school math requirement with these alternative classes. As the author sees it, this would limit “misdirecting precious resources” presumably by redirecting them to the new classes. Does that mean we abandon the majority of students who can pass traditional algebra to the ineffective mores of a failing system (now with even fewer resources) because, hey, at least they’re not struggling? Never mind the fact that neither are they soaring as high as they could and will need to as the influence of technology on their world grows!

Teaching mathematics effectively to all students is the outcome we should be striving toward. Make no mistake—we understand the consequences of the prolonged economic stress on families, school districts, and public higher education. It is natural in such times to direct limited resources to activities most likely to lead to gainful employment. So let’s consider a key element of the author’s argument—that high schools are not even teaching students the math skills they will need in the workplace. He writes:

The author seems to miss the point that the mathematical reasoning skills needed to succeed in the workplace are the same ones needed to succeed in algebra. In both cases, you must be able recognize a problem or challenge, gather information relevant to finding a solution, analyze and synthesize the information to derive a solution, and effectively apply the solution. This takes critical thinking and logical reasoning abilities, and the current pedagogical approach is to try to impart these skills through the process of teaching algebra, almost as a side-effect.

Were the US education system to focus more in elementary school on building these fundamental skills, not only would students find learning high school algebra (and learning in general) easier, they would also be better equipped to succeed in the workplace where problem solvers are highly valued. Furthermore, as learning algebra becomes easier, it becomes less time-consuming, thereby freeing up instructional time to add topics from skill-training to more advanced math as desired. It may sound like an idealistic vision to the millions of people who have come to believe they are “bad at math” when they are more likely the product of bad math curricula, but we have seen this approach work for IMACS students for over 20 years.

Of course considerable training occurs after hiring in STEM fields! The need for accuracy and the complexity of the body of knowledge are so much greater in these fields than in others that are more subjective in nature (e.g., the arts) or that rely more on so-called “soft skills” (e.g., politics). We need only to look to the history of the Space Shuttle to understand the consequences of errors in judgment. On a happier note, consider that the successful entry, descent, and landing of the Mars Science Laboratory was almost 10 years in the making. On-the-job training is necessary in many non-STEM fields from law to portfolio management to journalism to costume design. Why should we expect STEM be any different?

As for the Toyota-sponsored Machine Tool Mathematics class, the course catalog description is “An applied mathematics course designed for machinists which includes instruction and practice in algebraic and trigonometric operations. (2 hour lecture, 2 hour lab).” That doesn’t sound like the math is different from what is taught in high school. Rather it sounds more like the way the math is taught is different. With a hands-on lab, it actually sounds like fun! That is a huge distinction and goes back to our main point that we need to significantly change our approach to how we teach mathematics in the US.

At IMACS, we support the idea of schools using math curricula that accurately incorporate real-world examples that students care about. This approach helps put abstract concepts in context but, more importantly, gets students interested in learning and helps them understand how mathematics shapes our world. Those who appreciate mathematics in its pure and abstract form are pretty special people, but math should and can be accessible to the majority as well. There also need to be more options for visual-spatial learners who may not “get” math concepts when presented on a bland white board. Rather than redirecting limited resources to creating new alternative classes, the focus should be on redesigning the algebra curriculum (as well as those for elementary, middle, and the rest of high school math) to present mathematics for what it truly is, a deep discipline centered around simple but beautiful ideas, rather than a bunch of numbers, funny symbols, and boring algorithms.

“In an online world, colleges have to think hard about how they are going to take communication, which comes over the Web, and turn it into learning, which is a complex social and emotional process.”
-David Brooks, New York Times, May 3, 2012

Over the last 15 years, the advances in our ability to share information broadly and quickly have been nothing short of astounding. More recently, we have started to witness technology’s influence on education. As Peter Haskell, math department chairman at Virginia Tech, said in a recent article, “How could [computers] not change higher education? They’ve changed everything else.”

Computers are indeed changing higher education, as well as elementary and secondary school education. The Danville School District in Indiana announced that it will be piloting an iPad-based program to educate its students by ability level and not by the traditional grade levels. Many see technology as the much-longed-for solution to the 21st century, individualized education that creativity expert, Sir Ken Robinson, espouses.

IMACS has been grouping students by ability level and using technology to provide customized learning experiences for over 20 years, and we’ve learned much in the process. We understand why it is tempting to leverage existing technology, as is, to try to improve education—development costs are little to none, and the solution seems to “fit” the problem “well enough.” However, our experience tells us that a more thoughtful approach yields better outcomes for the students involved.

The popular approach to incorporating technology in education seems to follow the “defense-to-daily life” path. By this we mean that amazing inventions first created for military purposes made their way into daily life after people asked, “How else can this be used?” Examples include digital photography, which came from spy satellites, and the GPS in your car that keeps you from getting lost.

Within the education debate, the analogous line of reasoning is, “We have the technology to distribute and exchange information on a global scale at relatively low cost. Education, in its most basic form, is information. Therefore, technology can be used to widely deliver education. Technology also enables us to track and analyze massive amounts of data. Student performance is essentially data. Therefore, we can use technology to determine when an individual student has learned a topic and is ready to study the next topic.”

One obvious problem is that this approach relies on quantifiable student performance, the kind that computers know how to “think” about. What’s that? None other than answers to multiple choice questions, stand-alone numeric answers, or simplistic word answers. In other words, this approach to individualized learning uses the type of assessment you find with one-size-fits-all standardized testing, which we know does not effectively measure mastery.

Consider the ability to apply learning to novel situations, which is a component of mastery that is generally recognized as the highest of the so-called “learning outcomes.” How could standardized test-like questions ever measure the ability to recognize underlying parallels and to transfer skills acquired in one context to another? Educational technology, while still a net positive, has its limits. It’s hard to imagine a situation in which a computer could reliably grade an essay on “Compare and contrast the lifestyles of the middle class in Manila, Philippines, and Quito, Ecuador.”

For technology to deliver on the promise of turning out well-educated students in greater numbers, methods should be developed for automatic evaluation of student performance that go beyond the multiple-choice paradigm. This includes designing questions that truly test the depth of a student’s understanding, along with systems to assess the quality of answers to such questions. In other words, the technology should be made to fit the curriculum and not the other way around.

Taking this approach means that one does not have to compromise on curriculum development. One has the freedom to create original course material based on what is shown to be effective, knowing that the technology to support it will follow. This is one of our founding principles at IMACS, where we have been researching, developing, and implementing these technologies in our online mathematics and computer science courses since the beginning. The depth of understanding that our students develop leaves us confident that we made the right choice for them.

Education reformers must decide if they will use the building momentum to spread mediocrity all over the place, or if they will push for the bold change necessary to teach students the 21st century skills that they need. Students deserve better than to have the technological tail wag the pedagogical dog.

For innovative courses in gifted math and online computer science, try IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

In our prior blog post where we discussed the importance of effective teachers for gifted students, we also made the point that such teachers should be armed with higher quality curricula better geared toward bright kids. This week, we delve more deeply into what raises the quality of curricula and renders them more suitable for bringing out the best in talented students.

Fast Forward vs. Delve Deeper

Let’s start with the obvious. Gifted students often understand new information after having it explained to them once. This is in contrast to a typical student who benefits meaningfully from review and reinforcement of new topics. There may be times when gifted children benefit from review, but they generally find repetition unutterably boring. Consequently, bright kids who are subjected to curricula that emphasize review can develop a dislike for school or, in the worst case, of learning.

Advocates of free online resources often point to online technology as a remedy in situations like this because you can skip over the boring parts of a lesson and cover more topics. But who wants to spend time and mental energy searching through a lesson to avoid the repetitive parts? More importantly for talented children, are we really aiming for quantity of topics over quality of learning as a badge of honor for the brightest among us? Gifted students’ time would be better spent gaining a deeper understanding of a subject using material that was specifically designed with their ability level and thirst for knowledge in mind.

Challenge and Failure as Preparation for Success

Online curriculum development for talented students is about more than just going faster and avoiding repetition. It’s about presenting challenging ideas along with the appropriate interactive tools to explore and understand them. It’s about asking questions that require genuine thought to answer rather than just a cursory understanding—or worse, a simple memory—of something. It’s about asking questions in such a way that, in the process of determining the answer, the student’s understanding gets deeper.

Parents and administrators should recognize that accelerating through standard curricula is not the same as studying coursework designed to challenge the gifted mind. Challenging talented students is essential for putting them on a path toward future success. These kids have the potential to solve our most intractable problems and invent products and processes not yet imagined. As anyone who has accomplished even one of these amazing feats will tell you—it’s not a sprint but a marathon fraught with many false turns. This relates to the much-quoted findings by Stanford psychologist Carol Dweck that praising intelligence undermines motivation and performance as compared with praising effort. A child who has not learned to put forth great effort in conquering ability-appropriate challenges or in developing resilience in the aftermath of failure will never reach his or her full potential.

Address Misunderstandings Immediately

For many subjects, including mathematics and computer science, ideas learned at one stage serve as the foundation for learning more complex ideas at later stages. Likewise, a misunderstanding of an earlier concept jeopardizes the understanding of future concepts that build upon it. It can be difficult to dislodge misconceptions that have had some time to settle:

Thus, any praiseworthy online education program should cause students to address a misunderstanding at the moment that they are having it. If you wait until some later time to give a student corrective feedback on their work, the moment of maximum learning has already passed. Remember that we’re talking about young students who are simultaneously learning various new ideas across multiple subjects. When a student is already focused on learning the next topic, it’s less effective to try to bring his or her mind back to an “old” idea.

How an online education program goes about detecting and addressing flaws in student understanding is critical to whether the program is really delivering on its promise to teach in the truest sense of the word. This is not a trivial exercise that can be accomplished by a system that instantly tells you whether a multiple choice selection or one-word answer is correct. Gifted kids can typically regurgitate information from memory or reflect back basic knowledge without much effort. But this doesn’t mean that they understand a topic at a depth commensurate with their ability. Any online curriculum that purports to educate yet relies on several, even many, simply structured questions as a measure of true understanding is short-changing its students, especially the bright ones.

Simply put, talented online students deserve curricula that address their unique intellectual needs along with technological tools designed to fit the particular curriculum and not the other way around. They deserve more than the same material they can get in school with improved presentation and a fast-forward button. Delivering on the promise of educating students online is possible, but it takes much more thought, planning, and investment to do than is widely accepted in the current media coverage and commentary.

Are you a gifted and talented middle or high school student? IMACS offers online courses designed just for you! Take our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.

IMACS pays tribute to Belgian mathematician and mathematics educator, Georges Papy, who died in Brussels this past November at the age of 91. Georges and his wife, Frédérique, also a noted mathematics educator, were two of the seminal figures in the development of what eventually became the IMACS Mathematics Enrichment curriculum. We are deeply grateful to the Papys for their life’s work on behalf of mathematics students and their teachers.

The Early Years

Georges Papy was born in Anderlecht, a municipality in Brussels, Belgium of not quite seven square miles, on November 4, 1920. World War I had ended just two years before, and the country, which had suffered immensely under four years of German occupation, was still recovering. Against this backdrop and coming of age during the rise of Hitler, it is no wonder that young Georges was a member of the armed underground resistance forces in Belgium during 1941 – 45, serving in particular in the areas of intelligence and action. An educator from the start, he taught clandestine courses to students at the University of Brussels during 1941 – 42, and taught in a clandestine school for Jews during 1942 – 43 in the town of Méan, 50 miles to the southeast of Brussels.

After the end of World War II, Papy earned his doctorate in mathematics (with the highest distinction) from the University of Brussels in 1945, and was granted his advanced teaching diploma by the Science Faculty of the University of Brussels in 1951. After serving from 1949 first as Reader and then as Senior Lecturer at the University of Brussels, he became Professor of Algebra in the Science Faculty in 1956. The year before, he became a member of the prestigious Institute for Advanced Study in Princeton, New Jersey.

Finding His Purpose: Mathematics Education

During the mid 1950s, influential academic mathematicians were leading efforts to improve the quality of mathematics education in France. In parallel with these developments, Georges became deeply interested in improving the quality of mathematics education at the secondary school level, and assumed a position of leadership in Belgium of what became known as the New Math movement. [This was inspired in part by a colloquium organized in 1959 in Royaumont, France, by the agency that in 1963 would become the OECD. A follow-up meeting held in Yugoslavia under the chairmanship of the American mathematician Marshall Stone gave rise to a secondary school mathematics curriculum that was published in Paris in 1961 under the name “Mathématiques nouvelles” (“New Math”).]

Papy’s work in mathematics education would accelerate quickly from that point. In 1961, he founded the Centre Belge de Pédagogie de la Mathématique (Belgian Center for Mathematics Pedagogy). From 1962 onward, Georges was called upon as an expert in mathematics education by several international groups, including UNESCO, IBM, and the OECD. During 1960 – 70, he served as president of the Commission Internationale pour l’Étude et l’Amélioration de l’Enseignement des Mathématiques (International Commission for the Study and Improvement of Mathematics Teaching), and was founding president of the Groupe International de Recherche en Pédagogie de la Mathématique (International Research Group in Mathematics Pedagogy), starting in 1970. Amid this flurry of activity, Papy even found time to serve as Senator in the Belgian government during 1963 – 64.

Modern Mathematics: A Crowning Achievement

During 1963 – 66, with the collaboration of his wife, Frédérique, Georges published the groundbreaking six-volume series entitled Mathématique Moderne (Modern Mathematics), which represented a fundamental reformation of the secondary school mathematics curriculum based upon the unifying themes of sets, relations, functions, and algebraic structures (such as groups).

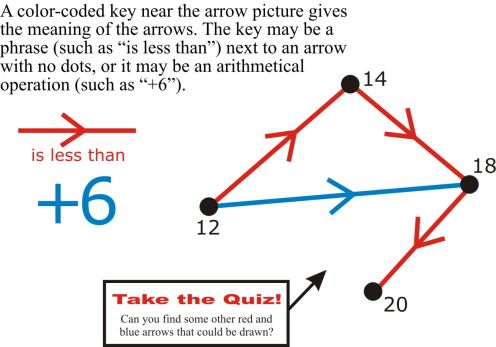
His mathematical educational interests expanded to include elementary school education. Starting in 1967, under the auspices of the CPBM, Frédérique and an associate taught experimental mathematics classes to six-year-olds. In the years that followed, Papy and Frédérique published several volumes comprising what amount to annotated accounts of these experimental classes and those that succeeded them. The mathematical underpinnings of this elementary school work remained the same as those of Papy’s earlier secondary school work, prominently featuring the use of multicolor arrow diagrams to represent relations and functions.

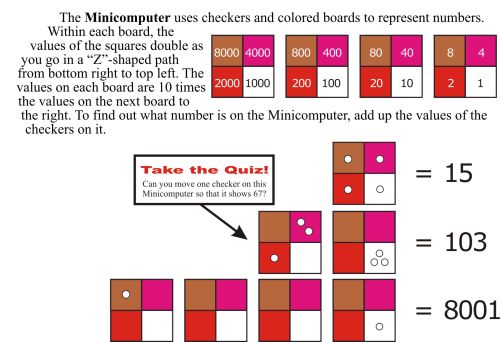
The Papy Minicomputer

As part of this work at the elementary school level, Papy developed what became known as the Papy Minicomputer and published a related text, Minicomputer, in 1968. This is a two-dimensional, mixed binary/decimal abacus made of square boards subdivided into four squares, each color-coded with Cuisenaire rod colors. He attributed the design of the Minicomputer to some work by the renowned Belgian cosmologist Msgr. Georges Lemaître (who was the first to propose what he called “The Primeval Atom” but which Fred Hoyle disparagingly labeled “The Big Bang Theory”). In the mid-1950s, Lemaître had proposed the introduction of new digits to represent numbers. The digits were formed from lines and curves that revealed an underlying binary structure. Papy adapted this idea and transformed it into a two-dimensional board on which checkers may be placed.

The IMACS Connection

In 1969, Georges and Frédérique met IMACS founder Burt Kaufman at the first conference run by the International Commission on Mathematics Education in Lyon, France. At the time, Burt was the director of a federally-funded mathematics curriculum research and development project called the Comprehensive School Mathematics Program. He managed to recruit Frédérique as his Director of Research, a role that she fulfilled during 1973 – 78. Of course, this meant that Georges paid frequent visits to the United States. Consequently, he and his wife had a very significant influence in setting the direction for the development of what has now become the IMACS Mathematics Enrichment curriculum.

Iain Ferguson works with an IMACS student to program a mobile robot.

Today, we’re chatting with Iain Ferguson who – in addition to being IMACS’s senior curriculum developer for the computer science program – is the guy behind the sophisticated technology that runs our online computer programming classes. Iain has taught these courses as well, and so brings with him the experience of having seen what works in the classroom and what doesn’t.

Q: Why does your Introduction to Computer Science course use the Scheme programming language? Isn’t the Advanced Placement exam in Java?

A: We start off with Scheme because it’s the most effective for helping students to understand the fundamental concepts of computer science that are common to all programming languages. And we’re not alone in this choice. Graduates of the some of the top universities, including MIT, Yale, Princeton, Johns Hopkins and UC Berkeley, were first taught to program in their freshman year using Scheme.

What we’ve found over 20 years of teaching this course is that if you throw a new student straight into Java, or whatever language the AP exam covers at the time, he or she can easily get mired in its complicated rules of syntax. If you simultaneously try to make a student learn the fundamentals, which are arguably more important, some of those fundamentals just won’t be understood, or they’ll be understood incorrectly. And so the students try to move on to more complicated programming assignments, and they’re hampered by a false understanding of the underlying abstract thinking.

Scheme’s syntax is simple and natural. So it takes our students very little time to pick it up. They use their mental energy instead on developing a deep comprehension of the the abstract mathematical thinking involved in programming. Applying that way of thinking to concrete computer algorithms is then rather trivial for them.

Q: Beyond doing well on the AP exam, how do you know that this approach of teaching Scheme first is working?

A: We hear from a lot of our former students once they’ve gone on to university about how easy their classes are thanks to what and how they learned here. One of my favorite stories is of a student named Erik who went to Virginia Tech. He was taking Computer Engineering in a class of about 600 students, and the first exam was designed to weed out about half of them. So Erik completed the test in 10 minutes with a perfect score. The next day the professor called him in and accused him of cheating. Well, of course, he hadn’t cheated and when he said so, the professor gave him a similar question that was solved just as quickly. Then the professor wanted to know how it was possible for a freshman to have such a deep understanding. Erik told him about learning to program with Scheme, and that was enough to convince the professor that not only had Erik not cheated but that he was also the strongest student in this class of 600.

Q: If Scheme is so beneficial, why don’t more high schools offer it?

A: Their resources are very limited, especially in this economic environment, and the demands on teachers’ time is rather significant. As with most university-level courses, it’s unrealistic to ask high schools to even consider putting resources towards preparing and teaching a class like this. If you really want to do it at a high level, you need instructors with an extensive background in university-level computer science and extensive training in teaching advanced subjects to young adults. Plus you either have to develop the appropriate curriculum or find it and license it. So you’re looking at a lot of time and expense, both of which are, unfortunately, in short supply at the typical high school.

Sounds like a guy who knows his stuff! What language did you use in your first computer programming class, and did it leave you with confusion or clarity?

P.S. If you’re ever in South Florida and want to play a game of Nim, stop by our offices and ask for Iain. He will destroy you, and it won’t hurt a bit!

Make IMACS a part of your program. Sign up for our free aptitude test. Follow IMACS on Facebook.

Terry Kaufman with student at the IMACS Hi-Tech Summer Camp Open House.

Welcome to the IMACS blog. Check in with us from time to time for mathematical musings and more. Since this is our inaugural blog post, we’ll be utterly predictable and start with the obligatory interview with the president. No, not that president. We mean our very own Terry Kaufman, president, co-founder and all-around good guy, at the Institute for Mathematics and Computer Science, lovingly known as IMACS.

Q: So, Terry, why did you start IMACS?

A: My dad, Burt Kaufman, had been working with mathematically talented students for as long as I can remember, whether it was developing curriculum or teaching them in the classroom. The programs he was involved with ultimately brought him back to South Florida where the Broward County public school system agreed to fund what was then called Mathematics Education for Gifted Secondary School Students (MEGSSS). Project MEGSSS had a successful run in Broward County from 1983 to 1993, but then fell to the budget cutting axe. Well, my oldest child was only two at the time, and I thought to myself, “You know, I really want him to have the benefit of this curriculum.” I’d seen with my own eyes the enthusiasm for math and computer science that my father’s students had when they studied this material. So I said to Ed [Martin] and Iain [Ferguson], our senior curriculum developers for math and computer science who were also teaching MEGSSS students at the time, “Let’s find a way to keep this thing going.” And IMACS was born, really out of a parent’s wish to have high quality math and computer science education available to his child.

Q: What’s the latest news at IMACS? What big goals are you and the team working towards?

A: We’re always working on new online computer courses. One initiative that we’re really excited about is our Online Virtual Robotics Lab in which students program robots in a virtual world. It’s entirely Web-based, but the actual physical behavior of real robots is accurately represented, even the appropriate laws of physics. What we’ve put together is a learning environment that integrates science, technology, engineering and math skills in a very natural way. Several schools are already using it as part of the national STEM Initiative, and we expect that number to grow.

Another of our programs that comes to mind is ISLAND, which stands for Interface for Scientific Learning & Natural Discovery. Here we use computer simulations and some really innovative online activities to encourage students to think scientifically and get involved in the learning process. Rather than simply being told dry scientific facts, they learn by doing – making hypotheses, observing simulations, and then developing scientific theories. They’re so engaged that they don’t realize they’re learning the required state standards. You know, people have traditionally thought of IMACS as a place for gifted and talented students, but the truth is that our teaching philosophy is really applicable to all students. With ISLAND, it’s been very gratifying to be able to share the benefits of our unique approach with a wider audience.

Q: Any message for the lucky folks who stumble upon this blog?

A: Yes! Read it. Share it. Tell us what you think. We are listening. There’s such a strong sense of community among our students, parents, teachers and alumni; it’s time we share that enthusiasm online. Obviously, we’d love for this blog and our Facebook page to be go-to places for people interested in taking online computer programming classes. But more importantly, we know from our many years of teaching mathematically talented students that we have a huge amount of knowledge in our heads on how to bring out the best in them, how to help them reach their full potential. Why keep it there? And we also know that our parents and students have great advice to give too. They share their stories with us face-to-face or in letters all the time. Now there are at least two places where these stories can find a wider audience and maybe help someone who is searching for this kind of information.

If you’ve read all the way to the end of this blog post, then our first attempt couldn’t have been all that bad! Do you have a topic to suggest for our blog? Leave a comment.

Find out if you’re ready for the IMACS experience. Sign up for our free aptitude test. Follow IMACS on Facebook.