Note: This story is adapted from the IMACS “Elements of Mathematics” series of textbooks and is based on modular arithmetic. This topic is typically covered in the first year of EM, which is often taught to talented 6th graders. The solution is revealed at the end of this post, so don’t scroll down too far if you want to avoid the spoiler!
The Stolen Jewel of Rainsmore
In the town of Rainsmore someone has stolen a precious jewel. A very famous detective, Roy Henshaw, has been called in to solve the crime. After a great deal of questioning, Detective Henshaw has narrowed the number of suspects to a small group.
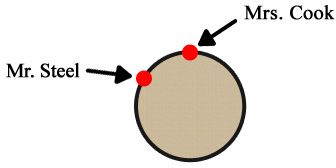
Late Wednesday night Henshaw seats the suspects around a table and begins questioning with Mr. Steel. Then he questions Mrs. Cook.
After Mrs. Cook has been questioned, Henshaw continues around the table in order, being very careful to skip no one and to ask each person a different question.
The questioning continues through the night with Henshaw getting closer to finding the thief.
By 5:00 in the morning Henshaw has asked hundreds of questions and, being such a famous detective, he has kept track of which questions each suspect has answered:
Mr. Steel has answered questions 1, 8, and 15.
Mr. Gunn has answered questions 3, 10, and 17.
Mr. Decker has answered questions 12, 19, and 26.
Mr. Jones has answered questions 11, 18, and 25.
Mrs. Cook has answered questions 2, 9, and 16.
Henshaw now has some important questions for which he needs answers. You should answer them if you are to solve the mystery.
a) How many people were seated around the table?
b) Who answered the 4th question?
c) Who answered the 5th question?
d) Who answered the 24th question?
e) Who answered the 31st question?
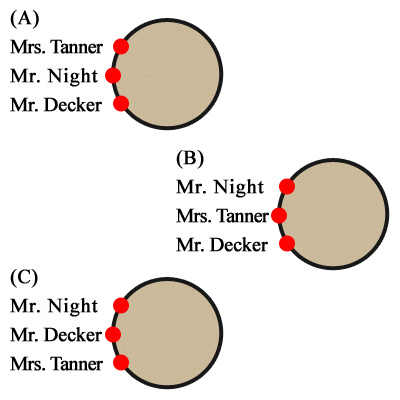
f) Detective Henshaw also noted that Mrs. Tanner answered question 70 and that Mr. Night answered question 48. Which of the following pictures shows the correct seating around the table of Mr. Night, Mrs. Tanner, and Mr. Decker?
g) Aha! Henshaw now knows who the thief is. His extremely clever and searching mind has unmasked the criminal.
THE CRIMINAL IS NONE OTHER THAN THE PERSON WHO ANSWERED THE 37TH QUESTION.
Who is the thief?
Has traditional school stolen your passion for learning? Find it again with engaging courses in gifted math and computer science online from IMACS! Register for our free aptitude test. Play along with our weekly IMACS logic puzzles on Facebook.
Answers:
a) Seven
b) Mr. Jones
c) Mr. Decker
d) Mr. Gunn
e) Mr. Gunn
f) Table (A)
g) Mrs. Cook
“In an online world, colleges have to think hard about how they are going to take communication, which comes over the Web, and turn it into learning, which is a complex social and emotional process.”
-David Brooks, New York Times, May 3, 2012
Over the last 15 years, the advances in our ability to share information broadly and quickly have been nothing short of astounding. More recently, we have started to witness technology’s influence on education. As Peter Haskell, math department chairman at Virginia Tech, said in a recent article, “How could [computers] not change higher education? They’ve changed everything else.”
Computers are indeed changing higher education, as well as elementary and secondary school education. The Danville School District in Indiana announced that it will be piloting an iPad-based program to educate its students by ability level and not by the traditional grade levels. Many see technology as the much-longed-for solution to the 21st century, individualized education that creativity expert, Sir Ken Robinson, espouses.
IMACS has been grouping students by ability level and using technology to provide customized learning experiences for over 20 years, and we’ve learned much in the process. We understand why it is tempting to leverage existing technology, as is, to try to improve education—development costs are little to none, and the solution seems to “fit” the problem “well enough.” However, our experience tells us that a more thoughtful approach yields better outcomes for the students involved.
The popular approach to incorporating technology in education seems to follow the “defense-to-daily life” path. By this we mean that amazing inventions first created for military purposes made their way into daily life after people asked, “How else can this be used?” Examples include digital photography, which came from spy satellites, and the GPS in your car that keeps you from getting lost.
Within the education debate, the analogous line of reasoning is, “We have the technology to distribute and exchange information on a global scale at relatively low cost. Education, in its most basic form, is information. Therefore, technology can be used to widely deliver education. Technology also enables us to track and analyze massive amounts of data. Student performance is essentially data. Therefore, we can use technology to determine when an individual student has learned a topic and is ready to study the next topic.”
One obvious problem is that this approach relies on quantifiable student performance, the kind that computers know how to “think” about. What’s that? None other than answers to multiple choice questions, stand-alone numeric answers, or simplistic word answers. In other words, this approach to individualized learning uses the type of assessment you find with one-size-fits-all standardized testing, which we know does not effectively measure mastery.
Consider the ability to apply learning to novel situations, which is a component of mastery that is generally recognized as the highest of the so-called “learning outcomes.” How could standardized test-like questions ever measure the ability to recognize underlying parallels and to transfer skills acquired in one context to another? Educational technology, while still a net positive, has its limits. It’s hard to imagine a situation in which a computer could reliably grade an essay on “Compare and contrast the lifestyles of the middle class in Manila, Philippines, and Quito, Ecuador.”
For technology to deliver on the promise of turning out well-educated students in greater numbers, methods should be developed for automatic evaluation of student performance that go beyond the multiple-choice paradigm. This includes designing questions that truly test the depth of a student’s understanding, along with systems to assess the quality of answers to such questions. In other words, the technology should be made to fit the curriculum and not the other way around.
Taking this approach means that one does not have to compromise on curriculum development. One has the freedom to create original course material based on what is shown to be effective, knowing that the technology to support it will follow. This is one of our founding principles at IMACS, where we have been researching, developing, and implementing these technologies in our online mathematics and computer science courses since the beginning. The depth of understanding that our students develop leaves us confident that we made the right choice for them.
Education reformers must decide if they will use the building momentum to spread mediocrity all over the place, or if they will push for the bold change necessary to teach students the 21st century skills that they need. Students deserve better than to have the technological tail wag the pedagogical dog.
For innovative courses in gifted math and online computer science, try IMACS! Register for our free aptitude test. Solve weekly IMACS logic puzzles on Facebook.